某商店经销一种奥运纪念品，据预测，在元旦后的20天内的每天销售量（件）与价格（元）均为时间t（天）的函数，且第t天的销售量近似满足g(t)＝80－2t（件），第t天的价格近似满足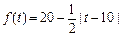
（元）．
（1）试写出该纪念品的日销售额y与时间t（0≤t≤20）的函数关系式；
（2）求该纪念品的日销售额y的最大值与最小值．
相关试题
），C（4，2），1＜m＜4。
，b＝4，且BC边上的高h＝
。
，若不等式
恒成立，求实数
的取值范围.
（
为参数）被曲线
所截的弦长.
，过顶点
的圆与边
切于
，与边
分别交于点
，且
，点
平分
.求证：
.
相关知识点
推荐套卷
某商店经销一种奥运纪念品，据预测，在元旦后的20天内的每天销售量（件）与价格（元）均为时间t（天）的函数，且第t天的销售量近似满足g(t)＝80－2t（件），第t天的价格近似满足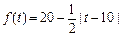（元）．
（1）试写出该纪念品的日销售额y与时间t（0≤t≤20）的函数关系式；
（2）求该纪念品的日销售额y的最大值与最小值．
粤公网安备 44130202000953号