（本小题满分12分）
设函数f(x)=ax+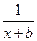
(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。
（Ⅰ）求f(x)的解析式：
（Ⅱ）证明：函数y=f(x)的图像是一个中心对称图形，并求其对称中心；
（Ⅲ）证明：曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值。
相关试题
中，
，
，
为
上的点，且
，
．
平面
；
平面
；
的体积．
中，
，
，
是
等比数列；（2）求数列
的前n项和。
的面积是30，内角
、
、
所对边长分别为
、
、
，
.
；(2)若
，求
.
，讨论
的单调性；
恒有
，求
的取值范围.
与x＝1时都取得极值.推荐套卷
（本小题满分12分）
设函数f(x)=ax+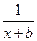(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。
（Ⅰ）求f(x)的解析式：
（Ⅱ）证明：函数y=f(x)的图像是一个中心对称图形，并求其对称中心；
（Ⅲ）证明：曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值。
粤公网安备 44130202000953号