已知椭圆C：
＋
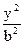＝1（a＞b＞0）的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点。
（1）求直线ON（O为坐标原点）的斜率KON ；
（2）对于椭圆C上任意一点M，试证：总存在角
（∈R）使等式：
＝cos
＋sin
成立。
相关试题
集合
.
,求
;
,求实数
的取值范围.
满足
（
为常数，
）
时，求
；
时，求
的值；
恒成立的常数
的前
项和
。
的最大或最小值．
中，角
，
，
所对的边分别是
，
，
，已知
，
．
，求
，求
，求建筑物AB和CD底部之间的距离BD。
推荐套卷
已知椭圆C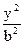：＋＝1（a＞b＞0）的离心率为，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点。
（1）求直线ON（O为坐标原点）的斜率KON ；
（2）对于椭圆C上任意一点M，试证：总存在角（∈R）使等式：＝cos＋sin成立。
粤公网安备 44130202000953号