某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为
，只选修甲和乙的概率是
，至少选修一门的概率是
，用
表示该学生选修的课程门数和没有选修的课程门数的乘积.
（1）记“函数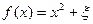
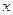为
上的偶函数”为事件
，求事件的概率；
（2）求的分布列和数学期望.
，求点Q的轨迹方程，并说明轨迹是什么曲线。推荐套卷
某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为，只选修甲和乙的概率是，至少选修一门的概率是，用表示该学生选修的课程门数和没有选修的课程门数的乘积.
（1）记“函数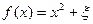 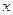为上的偶函数”为事件，求事件的概率；
（2）求的分布列和数学期望.
粤公网安备 44130202000953号