已知函数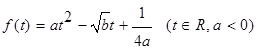 的最大值为正实数,集合
的最大值为正实数,集合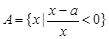 ,集合
,集合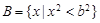 。
。
(1)求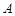 和
和 ;
;
(2)定义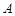 与
与 的差集:
的差集: 且
且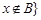 。
。
设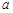 ,
, ,
,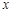 均为整数,且
均为整数,且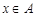 。
。 为
为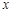 取自
取自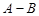 的概率,
的概率,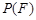 为
为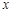 取自
取自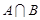 的概率,写出
的概率,写出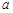 与
与 的二组值,使
的二组值,使 ,
, 。
。
(3)若函数 中,
中, ,
, 是(2)中
是(2)中 较大的一组,试写出
较大的一组,试写出 在区间[
在区间[ ,n]上的最 大值函数
,n]上的最 大值函数 的表达式。
的表达式。
推荐套卷
已知函数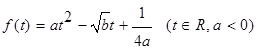 的最大值为正实数,集合
的最大值为正实数,集合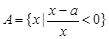 ,集合
,集合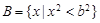 。
。
(1)求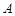 和
和 ;
;
(2)定义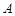 与
与 的差集:
的差集: 且
且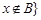 。
。
设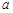 ,
, ,
,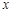 均为整数,且
均为整数,且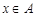 。
。 为
为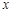 取自
取自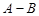 的概率,
的概率,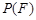 为
为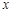 取自
取自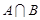 的概率,写出
的概率,写出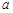 与
与 的二组值,使
的二组值,使 ,
, 。
。
(3)若函数 中,
中, ,
, 是(2)中
是(2)中 较大的一组,试写出
较大的一组,试写出 在区间[
在区间[ ,n]上的最 大值函数
,n]上的最 大值函数 的表达式。
的表达式。