某电视台在一次对文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关数据如下表所示:
|
文艺节目
|
新闻节目
|
总计
|
20岁到40岁
|
40
|
20
|
60
|
40岁以上
|
15
|
25
|
40
|
总计
|
55
|
45
|
100
|
(1)用分层抽样方法在收看新闻节目的观众中,随机抽取9名,那么40岁以上的观众应抽取几名?
(2)由表中数据分析,我们能否有99%的把握认为收看新闻节目的观众与年龄有关?(最后结果保留3位有效数字,四舍五入)
附: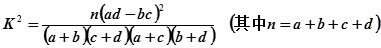
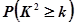
|
0.05
|
0.01
|
0.005
|
0.001
|

|
3.841
|
6.635
|
7.879
|
10.828
|