某商场为刺激消费,拟按以下方案进行促销:顾客每消费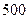 元便得到抽奖券一张,每张抽奖券的中奖概率为
元便得到抽奖券一张,每张抽奖券的中奖概率为 ,若中奖,商场返回顾客现金
,若中奖,商场返回顾客现金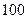 元.某顾客现购买价格为
元.某顾客现购买价格为 元的台式电脑一台,得到奖券
元的台式电脑一台,得到奖券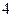 张.
张.
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为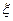 ,求
,求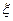 的分布列;
的分布列;
(Ⅱ)设该顾客购买台式电脑的实际支出为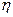 (元),用
(元),用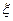 表示
表示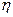 ,并求
,并求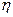 的数学期望.
的数学期望.
推荐套卷
某商场为刺激消费,拟按以下方案进行促销:顾客每消费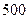 元便得到抽奖券一张,每张抽奖券的中奖概率为
元便得到抽奖券一张,每张抽奖券的中奖概率为 ,若中奖,商场返回顾客现金
,若中奖,商场返回顾客现金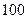 元.某顾客现购买价格为
元.某顾客现购买价格为 元的台式电脑一台,得到奖券
元的台式电脑一台,得到奖券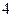 张.
张.
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为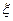 ,求
,求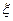 的分布列;
的分布列;
(Ⅱ)设该顾客购买台式电脑的实际支出为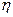 (元),用
(元),用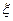 表示
表示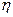 ,并求
,并求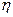 的数学期望.
的数学期望.