(本小题满分12分)如图，中心在原点O的椭圆的右焦点为F（3，0），
右准线l的方程为：x = 12。
（1）求椭圆的方程；(4分)
（2）在椭圆上任取三个不同点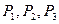
，使
，
证明: 
为定值，并求此定值。(8分)
|
中任选三个不同元素作为二次函数
的系数,问能组成多少条图像为经过原点且顶点在第一象限或第三象限的抛物线?
展开式中的常数项。
.
.推荐套卷
(本小题满分12分)如图，中心在原点O的椭圆的右焦点为F（3，0），
右准线l的方程为：x = 12。
（1）求椭圆的方程；(4分)
（2）在椭圆上任取三个不同点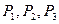，使，
证明: 为定值，并求此定值。(8分)
|
粤公网安备 44130202000953号