汽车在行驶中，汽油平均消耗率g(即每小时的汽油消耗量，单位：L/h)与汽车行驶的平均速度v（单位：km/h)之间有函数关系：g=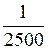
(v-50)2+5 (0<v<150).
“汽油的使用率最高”为每千米汽油平均消耗量最小（单位：L/km),则汽油的使用率最高时，汽车速度是 （km/h).
，则
；
，则
，-2），Q（-2
表示焦点在
轴上的椭圆，则
的取值范围是_____
的焦距是，焦点坐标为；若CD为过左焦点
的弦，则
的周长为
,焦点在y轴上的椭圆的标准方程是推荐套卷
汽车在行驶中，汽油平均消耗率g(即每小时的汽油消耗量，单位：L/h)与汽车行驶的平均速度v（单位：km/h)之间有函数关系：g=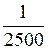 (v-50)2+5 (0<v<150).
“汽油的使用率最高”为每千米汽油平均消耗量最小（单位：L/km),则汽油的使用率最高时，汽车速度是 （km/h).
粤公网安备 44130202000953号