如图,椭圆C: 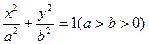 的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线
的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线 的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
(I)求证:切线l的斜率为定值;
(Ⅱ)若抛物线P与直线l及y轴围成的图形面积为 ,求抛物线P的方程;
,求抛物线P的方程;
(III)当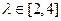 时,求椭圆离心率e的取值范围。
时,求椭圆离心率e的取值范围。
|
推荐套卷
如图,椭圆C: 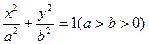 的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线
的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线 的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
(I)求证:切线l的斜率为定值;
(Ⅱ)若抛物线P与直线l及y轴围成的图形面积为 ,求抛物线P的方程;
,求抛物线P的方程;
(III)当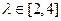 时,求椭圆离心率e的取值范围。
时,求椭圆离心率e的取值范围。
|