(本小题满分12分)已知抛物线 的准线方程
的准线方程 ,
, 与直线
与直线 在第一象限相交于点
在第一象限相交于点 ,过
,过 作
作 的切线
的切线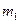 ,过
,过 作
作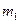 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点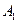 ,过
,过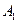 作
作 的平行线
的平行线 交抛物线
交抛物线 于第一象限内的点
于第一象限内的点 ,过
,过 作抛物线
作抛物线 的切线
的切线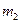 ,过
,过 作
作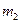 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点 ,…,依此类推,在x轴上形成一点列
,…,依此类推,在x轴上形成一点列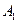 ,
, ,
, ,…,
,…, ,设点
,设点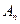 的坐标为
的坐标为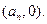
(Ⅰ)试探求 关于
关于 的递推关系式; (Ⅱ)求证:
的递推关系式; (Ⅱ)求证: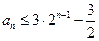 ;
;
(Ⅲ)求证: .
.
推荐套卷
(本小题满分12分)已知抛物线 的准线方程
的准线方程 ,
, 与直线
与直线 在第一象限相交于点
在第一象限相交于点 ,过
,过 作
作 的切线
的切线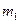 ,过
,过 作
作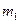 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点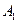 ,过
,过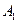 作
作 的平行线
的平行线 交抛物线
交抛物线 于第一象限内的点
于第一象限内的点 ,过
,过 作抛物线
作抛物线 的切线
的切线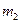 ,过
,过 作
作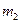 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点 ,…,依此类推,在x轴上形成一点列
,…,依此类推,在x轴上形成一点列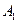 ,
, ,
, ,…,
,…, ,设点
,设点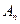 的坐标为
的坐标为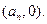
(Ⅰ)试探求 关于
关于 的递推关系式; (Ⅱ)求证:
的递推关系式; (Ⅱ)求证: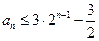 ;
;
(Ⅲ)求证: .
.