如图直棱柱ABC-A1B1C1中AB=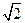
,AC=3,BC=
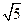,D是A1C的中点E是侧棱BB1上的一动点。
(1)当E是BB1的中点时，证明：DE//平面A1B1C1；
(2)求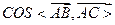
的值
(3)在棱 BB1上是否存在点E,使二面角E-A1C-C是直二面角？若存在求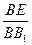
的值，不存在则说明理由。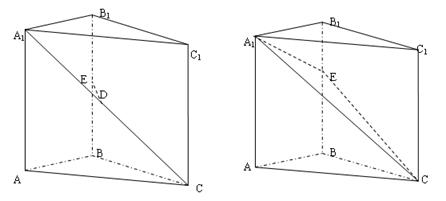
相关试题
上的函数
，对任意的
有
，且
．
的值； 
，使
，试问
中，
，
，
．
；
，
，求三棱柱
和矩形
所在的平面互相垂直，
，
，
是线段
的中点．
的体积；
//平面
;
＝
，
＝
，试用
。
中，
底面
，
，点
在线段
上，且
平面
;
，
，
，
，求四棱锥推荐套卷
如图直棱柱ABC-A1B1C1中AB=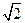,AC=3,BC=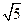,D是A1C的中点E是侧棱BB1上的一动点。
(1)当E是BB1的中点时，证明：DE//平面A1B1C1；
(2)求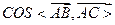的值
(3)在棱 BB1上是否存在点E,使二面角E-A1C-C是直二面角？若存在求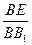的值，不存在则说明理由。
粤公网安备 44130202000953号