设圆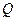
过点P(0,2), 且在
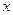轴上截得的弦RG的长为4.
(１)求圆心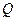的轨迹E的方程；
(２)过点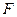
(０，１)，作轨迹
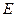的两条互相垂直的弦
、
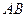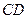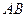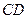，设、 的中点分别为
、
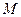，试判断直线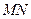
是否过定点？并说明理由．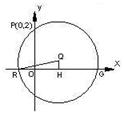
相关试题
与
的交点P，
的直线
的方程;
与直线
垂直,求
.
经过点(0，－2)，其倾斜角是60°．
,离心率
.
与椭圆交于不同的两点
，且线段
的中点的横坐标为
，求直线
的各项均为正数，
，前
项和为
，
为等比数列, 
，且
．
与
； (2)求和：
．推荐套卷
设圆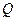过点P(0,2), 且在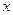轴上截得的弦RG的长为4.
(１)求圆心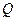的轨迹E的方程；
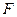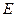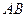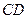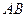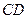(２)过点(０，１)，作轨迹的两条互相垂直的弦、，设、 的中点分别为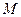、，试判断直线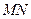是否过定点？并说明理由．
粤公网安备 44130202000953号