已知函数
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a,b的关系；
(Ⅱ) 说明函数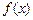
可以在
和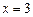
时取得极值，并求此时a,b的值；
(Ⅲ) 在满足(2)的条件下，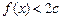
在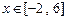
恒成立，求c的取值范围.
在 
时的值域(其中
为常数)
的方程
的两根为
和
：(12分)
的值；
的值．
,求
的值.
推荐套卷
已知函数的图象为曲线E.
(Ⅰ) 若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a,b的关系；
(Ⅱ) 说明函数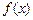可以在和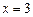时取得极值，并求此时a,b的值；
(Ⅲ) 在满足(2)的条件下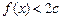，在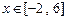恒成立，求c的取值范围.
粤公网安备 44130202000953号