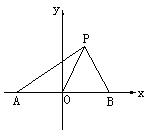如图,在直角坐标系中,点A(-1,0),B(1,0),P(x,y)(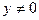 )。设
)。设 与x轴正方向的夹角分别为α、β、γ,若
与x轴正方向的夹角分别为α、β、γ,若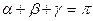 。
。
(I)求点P的轨迹G的方程;
(II)设过点C(0,-1)的直线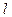 与轨迹G交于不同两点M、N。问在x轴上是否存在一点
与轨迹G交于不同两点M、N。问在x轴上是否存在一点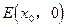 ,使△MNE为正三角形。若存在求出
,使△MNE为正三角形。若存在求出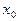 值;若不存在说明理由。
值;若不存在说明理由。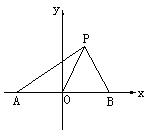
推荐套卷
如图,在直角坐标系中,点A(-1,0),B(1,0),P(x,y)(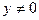 )。设
)。设 与x轴正方向的夹角分别为α、β、γ,若
与x轴正方向的夹角分别为α、β、γ,若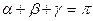 。
。
(I)求点P的轨迹G的方程;
(II)设过点C(0,-1)的直线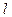 与轨迹G交于不同两点M、N。问在x轴上是否存在一点
与轨迹G交于不同两点M、N。问在x轴上是否存在一点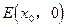 ,使△MNE为正三角形。若存在求出
,使△MNE为正三角形。若存在求出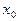 值;若不存在说明理由。
值;若不存在说明理由。