如图所示, 在三棱柱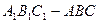 中,
中, 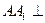 底面
底面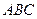 ,
,
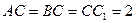 .
.
(1)若点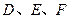 分别为棱
分别为棱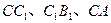 的中点,求证:
的中点,求证: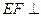 平面
平面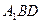 ;
;
(2) 请根据下列要求设计切割和拼接方法:要求用平行于三棱柱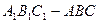 的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).
的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).
推荐套卷
如图所示, 在三棱柱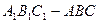 中,
中, 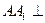 底面
底面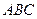 ,
,
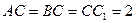 .
.
(1)若点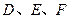 分别为棱
分别为棱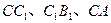 的中点,求证:
的中点,求证: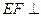 平面
平面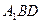 ;
;
(2) 请根据下列要求设计切割和拼接方法:要求用平行于三棱柱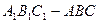 的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).
的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).