）某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛胜场的事件是独立的，并且胜场的概率是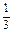
.
（1）求这支篮球队首次胜场前已经负了两场的概率；
（2）求这支篮球队在6场比赛中恰好胜了3场的概率；
（3）求这支篮球队在6场比赛中胜场数的期望和方差.
是一次函数，满足
，求
，
组成，若
，求x．
，x∈R，试讨论f（x）的奇偶性，并求f（x）的最小值．
，求当x
0时，f（x）的解析式．
,求a的取值范围．相关知识点
推荐套卷
）某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛胜场的事件是独立的，并且胜场的概率是.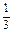
（1）求这支篮球队首次胜场前已经负了两场的概率；
（2）求这支篮球队在6场比赛中恰好胜了3场的概率；
（3）求这支篮球队在6场比赛中胜场数的期望和方差.
粤公网安备 44130202000953号