某个命题与正整数 有关,若
有关,若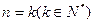 时该命题成立,那么可推得
时该命题成立,那么可推得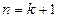 时该命题也成立,现在已知当
时该命题也成立,现在已知当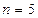 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A.当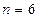 时,该命题不成立 时,该命题不成立 |
B.当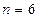 时,该命题成立 时,该命题成立 |
C.当 时,该命题不成立 时,该命题不成立 |
D.当 时,该命题成立 时,该命题成立 |
相关知识点
推荐套卷
某个命题与正整数 有关,若
有关,若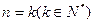 时该命题成立,那么可推得
时该命题成立,那么可推得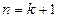 时该命题也成立,现在已知当
时该命题也成立,现在已知当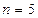 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A.当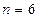 时,该命题不成立 时,该命题不成立 |
B.当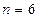 时,该命题成立 时,该命题成立 |
C.当 时,该命题不成立 时,该命题不成立 |
D.当 时,该命题成立 时,该命题成立 |