已知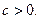
设P：函数
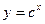在R上单调递减； Q：不等式
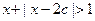的解集为R，若“P或Q”是真命题，“P且Q”是假命题，求
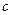的取值范围.
[解题思路]：“P或Q”是真命题，“P且Q”是假命题，根据真假表知，P，Q之中一真一假，因此有两种情况，要分类讨论.
相关试题
且满足
.
求△ABC的面积.
的前n项和为
，且
.
，求数列
的前
项和
.
且
.
的值；
的值.
是等差数列，且
.
，求数列
的前10项和．
，c=1，
，求a，A，C．相关知识点
推荐套卷
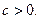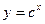已知 设P：函数在R上单调递减； Q：不等式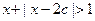的解集为R，若“P或Q”是真命题，“P且Q”是假命题，求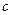的取值范围.
[解题思路]：“P或Q”是真命题，“P且Q”是假命题，根据真假表知，P，Q之中一真一假，因此有两种情况，要分类讨论.
粤公网安备 44130202000953号