近年来,我国很多城市都出现了严重的雾霾天气.为了更好地保护环境,2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
组别
|
PM2.5浓度(微克/立方米)
|
频数(天)
|
第一组
|
(0,35]
|
24
|
第二组
|
(35,75]
|
48
|
第三组
|
(75,115]
|
12
|
第四组
|
>115
|
6
|
(1)在这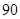 天中抽取
天中抽取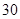 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?
(2)在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.