定义在R上的函数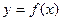
，
，当x＞0时，
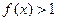，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.
（1）求证：f（0）=1；
（2）求证：对任意的x∈R，恒有f（x）＞0；
（3）求证：f（x）是R上的增函数；
（4）若f（x）·f（2x－x2）＞1，求x的取值范围.
，
；
，
，
（n∈N*）；
，
；
，
和集合
各有12个元素，
含有4个元素，试求同时满足下面两个条件的集合
的个数：
，且
（
表示空集）
，若
恒成立，求
的值域
的定义域是
，求函数
的定义域
的定义域为
，求
的定义域推荐套卷
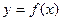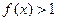定义在R上的函数，，当x＞0时，，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.
（1）求证：f（0）=1；
（2）求证：对任意的x∈R，恒有f（x）＞0；
（3）求证：f（x）是R上的增函数；
（4）若f（x）·f（2x－x2）＞1，求x的取值范围.
粤公网安备 44130202000953号