(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)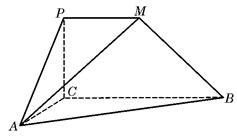 如图,
如图,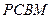 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又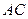 =1,∠
=1,∠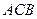 =120°,
=120°,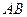 ⊥
⊥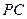 ,直线
,直线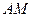 与直线
与直线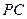 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面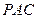 ⊥平面
⊥平面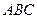 ;
;
(Ⅱ)求二面角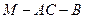 的大小;
的大小;
(Ⅲ)求三棱锥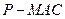 的体积.
的体积.
推荐套卷
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分) 如图,
如图,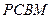 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又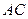 =1,∠
=1,∠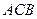 =120°,
=120°,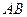 ⊥
⊥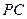 ,直线
,直线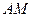 与直线
与直线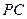 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面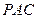 ⊥平面
⊥平面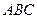 ;
;
(Ⅱ)求二面角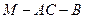 的大小;
的大小;
(Ⅲ)求三棱锥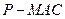 的体积.
的体积.