已知椭圆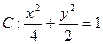
和圆
，且圆C与x轴交于A1，A2两点（1）设椭圆C1的右焦点为F，点P的圆C上异于A1，A2的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明。 （2）设点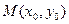
在直线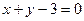
上，若存在点
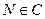，使得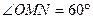
（O为坐标原点），求
的取值范围。
相关试题
，
是⊙
的一条切线，切点为
，
都是⊙
；
.
，
．
的单调区间；
在区间（0,+
上恒成立，求
的取值范围；
．
（
）．
过点
，求曲线
处的切线方程；
在区间
上的最大值．
满足
，
，
，其中
． 
为等比数列；
的前
项和
.
中，底面
为菱形，
，
，点
在线段
上，且
,
为
的中点.
平面
；
平面
，求三棱锥
的体积；
平面
的平面角的正切值.推荐套卷
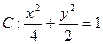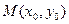已知椭圆和圆，且圆C与x轴交于A1，A2两点（1）设椭圆C1的右焦点为F，点P的圆C上异于A1，A2的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明。 （2）设点在直线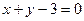上，若存在点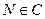，使得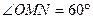（O为坐标原点），求的取值范围。
粤公网安备 44130202000953号