湘教版选修1-1 2.1 椭圆练习卷
已知椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(﹣10,0),则焦点坐标为( )
| A.(±13,0) | B.(0,±10) | C.(0,±13) | D.(0,± ) ) |
已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).
(1)求椭圆E的标准方程;
(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.
已知椭圆 =1的上焦点为F,直线x+y﹣1=0和x+y+1=0与椭圆分别相交于点A,B和C,D,则AF+BF+CF+DF=( )
=1的上焦点为F,直线x+y﹣1=0和x+y+1=0与椭圆分别相交于点A,B和C,D,则AF+BF+CF+DF=( )
A.2 |
B.4 |
C.4 | D.8 |
已知椭圆 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是 ,过椭圆上一点M作直线MA,MB分别交椭圆于A,B两点,且斜率分别为k1,k2,若点A,B关于原点对称,则k1•k2的值为( )
,过椭圆上一点M作直线MA,MB分别交椭圆于A,B两点,且斜率分别为k1,k2,若点A,B关于原点对称,则k1•k2的值为( )
A. |
B.﹣ |
C. |
D.﹣ |
如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆 的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为 .
的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为 .




 ,0),(
,0),( ,则椭圆C的方程为( )
,则椭圆C的方程为( ) +y2=1
+y2=1 =1
=1 =1
=1 +
+ =1
=1 ,则此椭圆的标准方程是 .
,则此椭圆的标准方程是 . 的离心率为
的离心率为 ,则k的值为 .
,则k的值为 . +y2=1的长轴和短轴的长、离心率、焦点和顶点的坐标.
+y2=1的长轴和短轴的长、离心率、焦点和顶点的坐标.

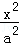 +
+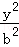 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
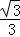
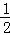
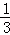
 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 .
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 . ,离心率为
,离心率为 的椭圆的标准方程为 .
的椭圆的标准方程为 .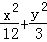 =1的焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是( )
=1的焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是( )
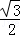
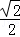

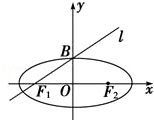

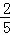
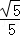

 =1有两个公共点,则m的取值范围是 .
=1有两个公共点,则m的取值范围是 . x+1截得的弦长为 .
x+1截得的弦长为 . +y2=1交于M、N两点,且|MN|=
+y2=1交于M、N两点,且|MN|= .求直线l的方程.
.求直线l的方程. +y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若 =3
=3 ,则|
,则| |=( )
|=( )

 +
+ =1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=12,则|AB|= .
=1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=12,则|AB|= . =1交于点B、C,当直线l绕点A(﹣1,1)旋转时,求弦BC中点M的轨迹方程.
=1交于点B、C,当直线l绕点A(﹣1,1)旋转时,求弦BC中点M的轨迹方程. +
+ =1长轴的左、右焦点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.
=1长轴的左、右焦点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号