江苏省常熟市八年级下学期期末考试数学试卷
若二次根式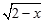 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
| A.x<2 | B.x≠2 | C.x≤2 | D.x≥2 |
正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图形的是( )
| A.正三角形 | B.正方形 | C.等腰直角三角形 | D.平行四边形 |
对于函数y= ,下列说法错误的是( )
,下列说法错误的是( )
| A.它的图像分布在第一、三象限 |
| B.它的图像与直线y=-x无交点 |
| C.当x>0时,y的值随x的增大而增大 |
| D.当x<0时,y的值随x的增大而减小 |
关于频率与概率有下列几种说法:( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为 ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为 ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在 附近,正确的说法是
附近,正确的说法是
| A.①④ | B.②③ | C.②④ | D.①③ |
如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )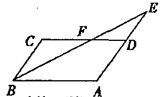
A. |
B.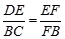 |
C.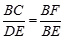 |
D.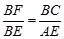 |
如图,矩形AOBC中,顶点C的坐标(4,2),又反比例函数y= 的图像经过矩形的对角线的交点P,则该反比例函数关系式是( )
的图像经过矩形的对角线的交点P,则该反比例函数关系式是( )
A.y=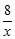 (x>0) (x>0) |
B.y=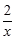 (x>0) (x>0) |
C.y=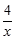 (x>0) (x>0) |
D.y= (x>0) (x>0) |
如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A'处,若A'为CE的中点,则折痕DE的长为( )
| A.1 | B.2 | C.4 | D.6 |

小丽同学想利用树影测量校园内的树高,她在某一时刻测得小树高为1.5m时,其影长为1.2 m,此时她测量教学楼旁的一棵大树影长为5m,那么这棵大树高约 m.
如图,在△ABC中,∠ACB=90°,∠A=35°,若以点C为旋转中心,将△ABC旋转θ°到△DEC的位置,使点B恰好落在边DE上,则θ值等于 .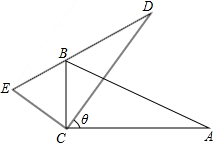
如图,等腰梯形ABCD中,AD∥BC,AD=2,BC=4,高DF=2.腰DC的长等于 .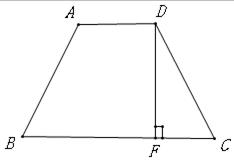
如图,点A、B在反比例函数y=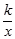 (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,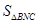 =2,则k的值为 .
=2,则k的值为 .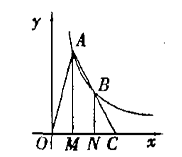
如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
如图,“优选1号”水稻的实验田是边长为a m(a>1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分;“优选2号”水稻的实验田是边长为(a-1)m的正方形,两块试验田的水稻都收了600 kg.
(1)优选 号水稻的单位面积产量高;
(2)“优选2号”水稻的单位面积产量是“优选1号”水稻的单位面积产量的多少倍?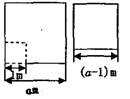
如图,在□ABCD中,点E在BC上,∠CDE=∠DAE.
(1)求证:△ADE∽△DEC;
(2)若AD=6,DE=4,求BE的长.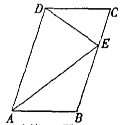
“初中生骑电动 车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了的统计图,请回答下列问题:
(1)这次抽查的家长总人数是多少?
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生,则抽到持哪一类态度学生的可能性大?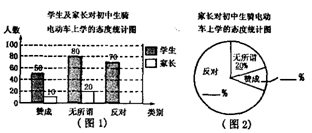
已知
(1)求 的值;
的值;
(2)将如图等腰三角形纸片沿底边BC上的高AD剪成两个三角形,其中AB=AC=m,BC=n.用这两个三角形你能拼成多少种平行四边形?分别求出它们对角线的长(画出所拼成平行四边形的示意图)
如图,在平面直角坐标系中,双曲线经过点B,连结OB.将OB绕点O按顺时针方向旋转90°并延长至A,使OA=2OB,且点A的坐标为(4,2).
(1)求过点B的双曲线的函数关系式;
(2)根据反比例函数的图像,指出当x<-1时,y的取值范围;
(3)连接AB,在该双曲线上是否存在一点P,使得S△ABP=S△ABO,若存在,求出点P坐标;若不存在,请说明理由.
喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
如图①,两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形,对角线均在坐标轴上,已知菱形EFGH与菱形ABCD的相似比为1:2,∠BAD=120°,其中AD=4.
(1)点D坐标为 ,点E坐标为 ;
(2)固定图①中的菱形ABCD,将菱形EFCH绕O点顺时针方向旋转α度角(0°<α<90°),并延长OE交AD于P,延长OH交CD于Q,如图②所示,
①当α=30°时,求点P的坐标;
②试探究:在旋转的过程中是否存在某一角度α,使得四边形AFEP是平行四边形?若存在,请推断出α的值;若不存在,说明理由;
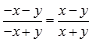


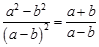
 是同类二次根式的是( )
是同类二次根式的是( )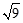
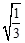


 的值为( )
的值为( )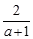 有意义,则a的取值范围是 .
有意义,则a的取值范围是 . = .
= . 是整数,则n的最小值是 .
是整数,则n的最小值是 .

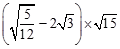
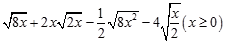
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号