[甘肃]2014年初中毕业升学考试(甘肃兰州卷)数学
下列说法中错误的是( )
| A.掷一枚均匀的骰子,骰子停止转动后6点朝上是必然事件 |
| B.了解一批电视机的使用寿命,适合用抽样调查的方式 |
| C.若a为实数,则|a|<0是不可能事件 |
D.甲、乙两人各进行10次射击,两人射击成绩的方差分别为 =2, =2, =4,则甲的射击成绩更稳定 =4,则甲的射击成绩更稳定 |
期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映处的统计量是( )
| A.众数和平均数 | B.平均数和中位数 |
| C.众数和方差 | D.众数和中位数 |
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cosA的值等于( )
A. |
B. |
C. |
D. |
下列命题中正确的是( )
| A.有一组邻边相等的四边形是菱形 |
| B.有一个角是直角的平行四边形是矩形 |
| C.对角线垂直的平行四边形是正方形 |
| D.一组对边平行的四边形是平行四边形 |
两圆的半径分别为2cm,3cm,圆心距为2cm,则这两个圆的位置关系是( )
| A.外切 | B.相交 | C.内切 | D.内含 |
一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则b2﹣4ac满足的条件是( )
| A.b2﹣4ac=0 | B.b2﹣4ac>0 | C.b2﹣4ac<0 | D.b2﹣4ac≥0 |
把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
| A.y=﹣2(x+1)2+2 | B.y=﹣2(x+1)2﹣2 |
| C.y=﹣2(x﹣1)2+2 | D.y=﹣2(x﹣1)2﹣2 |
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为( )
A. |
B. |
C. |
D.π |
如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.AE=BE B. =
= C.OE=DE D.∠DBC=90°
C.OE=DE D.∠DBC=90°
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
| A.c>0 | B.2a+b=0 | C.b2﹣4ac>0 | D.a﹣b+c>0 |
如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )




A B C D
在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于 .
如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为 .
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+3+32+33+…+32014的值是 .
(1)计算:(﹣1)2﹣2cos30°+ +(﹣2014)0;
+(﹣2014)0;
(2)当x为何值时,代数式x2﹣x的值等于1.
如图,在△ABC中,先作∠BAC的角平分线AD交BC于点D,再以AC边上的一点O为圆心,过A、D两点作⊙O(用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
| 时间(小时) |
频数(人数) |
频率 |
| 0≤t<0.5 |
4 |
0.1 |
| 0.5≤t<1 |
a |
0.3 |
| 1≤t<1.5 |
10 |
0.25 |
| 1.5≤t<2 |
8 |
b |
| 2≤t<2.5 |
6 |
0.15 |
| 合计 |
|
1 |
(1)在图1中,a= ,b= ;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
如图,直线y=mx与双曲线y=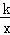 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>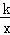 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.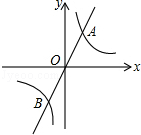
如图,AB是⊙O的直径,点E是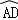 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.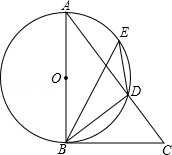
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.




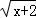 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) 的图象位于第二、四象限,则k的取值可以是( )
的图象位于第二、四象限,则k的取值可以是( ) =0,那么菱形的面积等于 .
=0,那么菱形的面积等于 .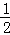 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).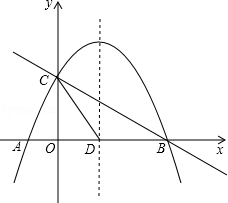
 粤公网安备 44130202000953号
粤公网安备 44130202000953号