重庆市高三下学期考前模拟(二诊)理科数学试卷
如图是收集重庆市2013年9月各气象采集点处的平均气温(单位:℃)的数据制成的频率分布直方图,图中有一处因污迹看不清。已知各采集点的平均气温范围是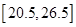 ,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )
,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )
| A.6 | B.7 | C.8 | D.9 |
某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为( )
| A.1 | B. |
C. |
D.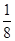 |
设 是椭圆
是椭圆 上两点,点
上两点,点 关于
关于 轴的对称点为
轴的对称点为 (异于点
(异于点 ),若直线
),若直线 分别交
分别交 轴于点
轴于点 ,则
,则 ( )
( )
| A.0 | B.1 | C. |
D.2 |
已知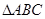 中,
中, 边的中点,过点
边的中点,过点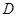 的直线分别交直线
的直线分别交直线 、
、 于点
于点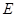 、
、 ,若
,若 ,
, ,其中
,其中 ,则
,则 的最小值是( )
的最小值是( )
| A.1 | B.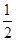 |
C.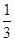 |
D. |
已知平面区域 ,直线
,直线 和曲线
和曲线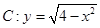 有两个不同的交点,直线
有两个不同的交点,直线 与曲线
与曲线 围成的平面区域为
围成的平面区域为 ,向区域
,向区域 内随机投一点
内随机投一点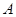 ,点
,点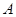 落在区域
落在区域 内的概率为
内的概率为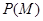 ,若
,若 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
在直角坐标系 中,以原点
中,以原点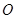 为极点,
为极点, 轴的正半轴为极轴建立极坐标系。已知直线
轴的正半轴为极轴建立极坐标系。已知直线 (
( 为参数)与曲线
为参数)与曲线 异于点
异于点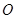 的交点为
的交点为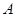 ,与曲线
,与曲线 异于点
异于点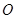 的交点为
的交点为 ,则
,则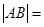 .
.
已知向量 ,函数
,函数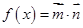 的最小正周期为
的最小正周期为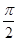 .
.
(1)求 的值;
的值;
(2)设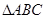 的三边
的三边 、
、 、
、 满足:
满足: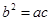 ,且边
,且边 所对的角为
所对的角为 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
某学校在一次运动会上,将要进行甲、乙两名同学的乒乓球冠亚军决赛,比赛实行三局两胜制.已知每局比赛中,若甲先发球,其获胜的概率为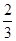 ,否则其获胜的概率为
,否则其获胜的概率为 .
.
(1)若在第一局比赛中采用掷硬币的方式决定谁先发球,试求甲在此局获胜的概率;
(2)若第一局由乙先发球,以后每局由负方先发球.规定胜一局记2分,负一局记0分,记 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
如图,直三棱柱 中,
中, ,
,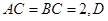 为
为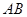 中点,
中点,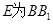 上一点,且
上一点,且 .
.
(1)当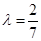 时,求证:
时,求证: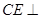 平面
平面 ;
;
(2)若直线 与平面
与平面 所成的角为
所成的角为 ,求
,求 的值.
的值.
已知椭圆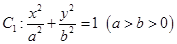 和椭圆
和椭圆 的离心率相同,且点
的离心率相同,且点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)设 为椭圆
为椭圆 上一点,过点
上一点,过点 作直线交椭圆
作直线交椭圆 于
于 、
、 两点,且
两点,且 恰为弦
恰为弦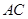 的中点。求证:无论点
的中点。求证:无论点 怎样变化,
怎样变化, 的面积为常数,并求出此常数.
的面积为常数,并求出此常数.
 为虚数单位,复数
为虚数单位,复数 的虚部是( )
的虚部是( )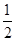
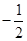

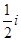
 ,集合
,集合 ,则
,则 ( )
( )
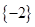

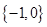
 是
是 的必要条件,
的必要条件, 是
是



 为( )
为( )
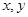 ,定义运算
,定义运算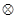 :
: ,设
,设 ,则
,则 的值是( )
的值是( )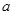


 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( )

 ,且
,且 ,则
,则 .
. 满足:对任意
满足:对任意 ,则公比
,则公比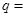 .
. 、
、 ,直线
,直线 与
与 分别与两圆交于点
分别与两圆交于点 、
、 和
和 、
、 ,
, ,则
,则 .
.
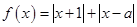 ,若不等式
,若不等式 的解集为
的解集为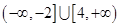 ,则实数
,则实数 的值为 .
的值为 . .
. ,当
,当 时,讨论
时,讨论 的单调性;
的单调性; 在
在 处取得极小值,求
处取得极小值,求 的取值范围.
的取值范围. 等分(
等分(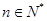 且
且 ),在相重叠的扇形格中依次同时填上
),在相重叠的扇形格中依次同时填上 ,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.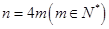 ,在如图所示的初始位置将任意
,在如图所示的初始位置将任意 对重叠的扇形格中的两数均改写为0,证明:当
对重叠的扇形格中的两数均改写为0,证明:当 时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号