湖北省襄阳市四校高二下学期期中联考文科数学试卷
命题“对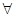
 ,都有
,都有 ”的否定为( )
”的否定为( )
A.对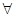 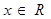 ,都有 ,都有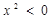 |
B.不存在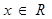 ,都有 ,都有 |
C.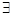 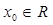 ,使得 ,使得 |
D.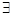 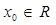 ,使得 ,使得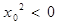 |
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
若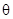 是任意实数,则方程
是任意实数,则方程 所表示的曲线一定不是( )
所表示的曲线一定不是( )
| A.直线 | B.双曲线 | C.抛物线 | D.圆 |
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
设函数 ,则( )
,则( )
A.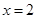 为 为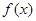 的极大值点 的极大值点 |
B.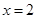 为 为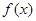 的极小值点 的极小值点 |
C.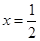 为 为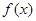 的极大值点 的极大值点 |
D.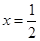 为 为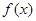 的极小值点 的极小值点 |
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
给定两个命题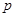 ,
,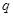 .若
.若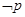 是
是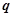 的必要而不充分条件,则
的必要而不充分条件,则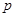 是
是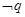 的( )
的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
已知点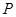 在曲线
在曲线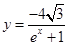 上,
上,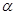 为曲线在点
为曲线在点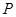 处的切线的倾斜角,则
处的切线的倾斜角,则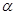 的取值范围是( )
的取值范围是( )
A.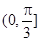 |
B.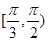 |
C. |
D.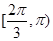 |
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
已知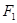 、
、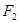 是椭圆
是椭圆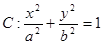 (
( >
>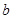 >0)的两个焦点,
>0)的两个焦点,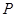 为椭圆
为椭圆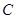 上一点,且
上一点,且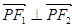 .若
.若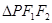 的面积为16,则
的面积为16,则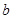 ="_________________;"
="_________________;"
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
过双曲线C: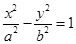
 的一个焦点作圆
的一个焦点作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,若
,若 (
(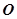 是坐标原点),则双曲线C的离心率为____;
是坐标原点),则双曲线C的离心率为____;
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
(已知双曲线的中心在坐标原点,焦点在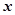 轴上,A是右顶点,B是虚轴的上端点,F是左焦点,
轴上,A是右顶点,B是虚轴的上端点,F是左焦点,
当BF⊥AB时,此类双曲线称为“黄金双曲线”,其离心率为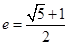 ,类比“黄金双曲线”,推算出“黄金椭圆”(如图)的离心率
,类比“黄金双曲线”,推算出“黄金椭圆”(如图)的离心率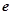 =_________;
=_________;
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其他费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其余费用为每小时1250元。
(1)把全程运输成本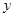 (元)表示为速度
(元)表示为速度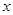 (海里/小时)的函数;
(海里/小时)的函数;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
来源:2013-2014学年湖北省襄阳市四校高二下学期期中联考文科数学试卷
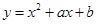 在点
在点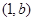 处的切线方程是
处的切线方程是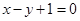 ,则( )
,则( )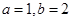
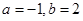
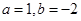
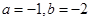
 有公共焦点,且离心率
有公共焦点,且离心率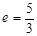 的双曲线方程是( )
的双曲线方程是( )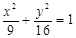

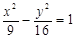

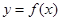 的图像如左图,则导函数
的图像如左图,则导函数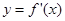 的图像可能是下图中的()
的图像可能是下图中的()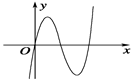
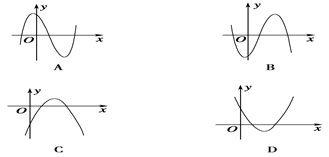
 的单调递增区间是( )
的单调递增区间是( )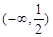
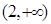
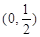
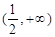
 表示焦点在
表示焦点在 轴上的椭圆,那么实数
轴上的椭圆,那么实数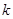 的取值范围是( )
的取值范围是( )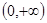

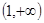

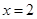 且
且 ,则
,则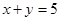 ”的逆否命题是_________命题;(填“真”或“假”)
”的逆否命题是_________命题;(填“真”或“假”) 的焦点坐标为_________________;
的焦点坐标为_________________; 在区间
在区间 上的最小值是_________________;
上的最小值是_________________;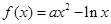 存在垂直于
存在垂直于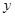 轴的切线,则实数
轴的切线,则实数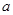 的取值范围是_______.
的取值范围是_______.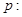 函数
函数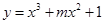 在
在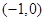 上是单调递减函数,
上是单调递减函数, 方程
方程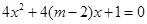 无实根,若“
无实根,若“ 或
或 ”为真,“
”为真,“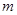 的取值范围。
的取值范围。 ,曲线
,曲线 在点
在点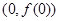 处切线方程为
处切线方程为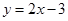 .
.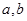 的值;
的值; 的单调性,并求
的单调性,并求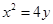 ,直线
,直线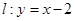 ,
,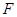 是抛物线的焦点。
是抛物线的焦点。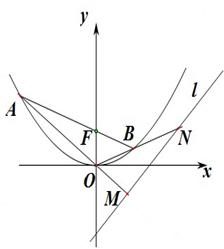
 ,使点
,使点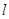 的距离最小;
的距离最小; ,求弦AB的长度;
,求弦AB的长度;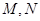 两点,求
两点,求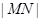 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号