河南省洛阳市高三上学期期末考试理科数学
已知全集U=(0,+∞),A={x|0<x<π},B={x| (x+1)>2},则A∩(CUB)=
(x+1)>2},则A∩(CUB)=
A.{x|0<x≤π} B.{x|-1<x≤π} C.{x|0<x≤3} D .{x|-1<x≤3}
.{x|-1<x≤3}
已知复数z=x+yi(x,y∈R),且有 =1+yi,
=1+yi, 是z的共轭复数,则
是z的共轭复数,则 =
=
A. - - i i |
B. + + i i |
C. + + i i |
D. - - i. i. |
设m、n是两条不同的直线,α、β是两个不重合的平面,则下列命题中正确的是
| A.若m∥α,m∥n,则n∥α | B.若m⊥α,n⊥β,则m⊥n |
| C.若m⊥α,m∥β,则α⊥β | D.若α⊥β,n α,则n⊥β α,则n⊥β |
.函数y=Asin(ωx+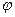 )(ω>0,|
)(ω>0,|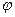 |<,x∈R)的部分图象如图所示,则该函数为
|<,x∈R)的部分图象如图所示,则该函数为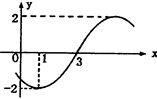
A.y=2sin(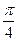 x+ x+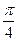 ) ) |
B.y=2sin(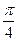 x- x-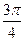 ) ) |
C.y=-2sin(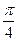 x- x-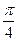 ) ) |
D.y=-2sin(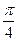 x+ x+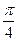 ) ) |
下列命题中的真命题的个数是
(1)命题“若x=1,则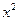 +x-2=0”的否命题为“若x=1,则
+x-2=0”的否命题为“若x=1,则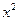 +x-2≠0”;
+x-2≠0”;
(2)若命题p: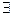 x0∈(-∞,0],
x0∈(-∞,0], ≥1,则
≥1,则 p:
p: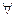 x∈(0,+∞),
x∈(0,+∞),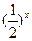 <1;
<1;
(3)设命题p: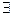 x0∈(-∞,0),
x0∈(-∞,0), <
<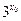 ,命题q:
,命题q: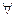 x∈(0,
x∈(0,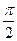 ),tanx>sinx,则(
),tanx>sinx,则( p)∧q为真命题;
p)∧q为真命题;
(4)设a,b∈R,那么“ab+1>a+b”是“ 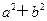 <1”的必要不充分条件.
<1”的必要不充分条件.
A. 0个 0个 |
B.1个 | C.2个 | D.3个 |
为欢庆元旦,某校高三年级一班、二班于12月30日在本班同时举办元旦文艺晚会,现有6名任课教师全部分配到这两班和同学们一起联欢,且每班最多安排4名教师,则不同的安排方法有
| A.50种 | B.70种 | C.35种 | D.55种 |
如图,△ABC中,|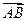 |=3,|
|=3,|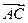 |=1,D是BC边中垂线上任意一点,则
|=1,D是BC边中垂线上任意一点,则 ·(
·(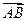 -
-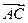 )
)
的值是
| A.1 | B.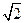 |
C.2 | D.4 |
已知函数f(x)是定义在R上的以4为周期的函数,”当x∈(-1,3]时,f(x)=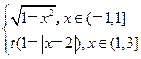 其中t>0.若函数y=
其中t>0.若函数y=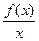 -
-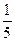 的零点个数是5,则t的取值范
的零点个数是5,则t的取值范
围为
A.(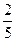 ,1) ,1) |
B.(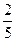 , ,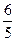 ) ) |
C.(1,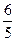 ) ) |
D.(1,+∞) |
设F1, F2分别为双曲线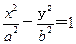 (a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若
(a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若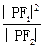 的最小值
的最小值 为8a,则该双曲线的离心率的取值范围是
为8a,则该双曲线的离心率的取值范围是
A.(1,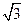 ] ] |
B.(1,3) | C.(1,3] | D.[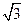 ,3) ,3) |
已知顶点在坐标原点的抛物线C的准线方程为y=-1,在[-1,1]上任取两个数a,b,那么点(a,b)在抛物线C上方的概率为_________________.
在△ABC中,∠BAC=45°,∠ACB=75°,D是∠ABC 平分线上的一点,且DB=DC.若BC=
平分线上的一点,且DB=DC.若BC=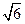 ,则AD=_______________.
,则AD=_______________.
(本小题满分12分)
设数列{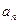 }的前n项和
}的前n项和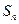 满足:
满足: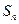 =n
=n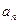 -2n(n-1).等比数列{
-2n(n-1).等比数列{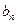 }的前n项和为
}的前n项和为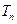 ,公比为
,公比为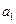
 ,且
,且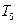 =
=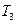 +2
+2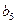 .
.
(1)求数列{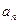 }的通项公式;
}的通项公式;
(2)设数列{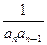 }的前n项和为
}的前n项和为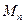 ,求证:
,求证: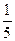 ≤
≤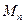 <
<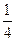 .
.
(本小题满分12分)
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,
AB=BC=2CD,PO⊥平面ABCD.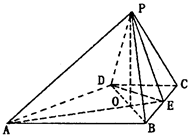
(1)求证:BD⊥PE;
(2)若AO=2PO,求二面角D-PE-B的余弦值.
(本小题满分12分)
某校高三一次月考之后,为了了解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成右面频率分布表: 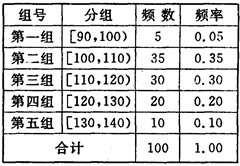
(1)若每组数据用该组区间的中点值(例如区间[90,100)的中点值是95)作为代表,试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在[110,130)中的学生数为ξ,求:
①在三次抽取过程 中至少有两次连续抽中成绩在[110,130)
中至少有两次连续抽中成绩在[110,130) 中的概率;
中的概率;
②ξ的分布列和数学期望.(注:本小题结果可用分数表示)
(本小题满分12分)
已知椭圆E: (a>b>0)的离心率e=
(a>b>0)的离心率e= ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2, ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上
(1)求椭圆E的方程;
(2)设l1,l2是过点G( ,0)且互相垂直的两条直线,l1交E于A,
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
(3)在(2)的条件下,设AB,CD的中点分别为M,N,试问直线MN是否恒过定点?
若经过 ,求出该定点坐标;若不经过,请说明理由。
,求出该定点坐标;若不经过,请说明理由。
(本小题满分12分)
设函数f(x)= +
+ -1.
-1.
(1)若x≥0时,f(x)≥0恒成立,求a的取值范围;
(2)求证:对于大于1的正整数n,恒有1+ <
< <1+
<1+ 成立.
成立.
(本小题满分10分)选修4-1:几何证明选讲
如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交 
AC于点D,设E为AB的中点.
(1)求证:直线DE为圆O的切线;
(2)设CE交圆O于点F,求证:CD·CA=CF·CE.
 在点(1,0)处的切线与直线x-ay+1=0垂直,则a=
在点(1,0)处的切线与直线x-ay+1=0垂直,则a=
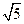 ,则tanα=
,则tanα=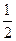
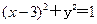 引切线,
引切线,  方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为____.
方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为____.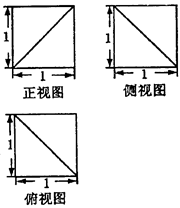
 粤公网安备 44130202000953号
粤公网安备 44130202000953号