临沂市费县七年级第二学期期末检测数学
永州市新田县的龙家大院至今已有930多年历史,因该村拥有保存完好的"三堂九井二十四巷四十八栋"明清建筑,而申报为中国历史文化名村.如图是龙家大院的一个窗花图案,它具有很好的对称美,这个图案是由:①正六边形;②正三角形;③等腰梯形;④直角梯形等几何图形构成,在这四种几何图形中既是轴对称图形又是中心对称图形的是___________(只填序号).

某商场开展购物抽奖促销活动,抽奖箱中有200张抽奖卡,其中有一等奖5张,二等奖10张,三等奖25张,其余抽奖卡无奖.某顾客购物后参加抽奖活动,他从抽奖箱中随机抽取一张,则中奖的概率为_________.
若点P 1(1,m),P 2(2,n)在反比例函数  的图象上,则m_____n(填">"、"<"或"="号).
的图象上,则m_____n(填">"、"<"或"="号).
如图,在⊙O中,直径CD垂直弦AB于点E,连接OB,CB,已知⊙O的半径为2,AB=  ,则∠BCD=________度.
,则∠BCD=________度.

某同学参加射击训练,共射击了六发子弹,击中的环数分别为3,4,5,7,7,10.则下列说法错误的是( )
| A. | 其平均数为6 | B. | 其众数为7 | C. | 其中位数为7 | D. | 其中位数为6 |
下列说法正确的是( )
| A. | 等腰梯形的对角线互相平分. |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形. |
| C. | 线段的垂直平分线上的点到线段两个端点的距离相等. |
| D. | 两边对应成比例且有一个角对应相等的两个三角形相似. |
由二次函数  ,可知( )
,可知( )
| A. | 其图象的开口向下 | B. |
其图象的对称轴为直线

|
| C. | 其最小值为1 | D. |
当
 时,y随x的增大而增大 时,y随x的增大而增大
|
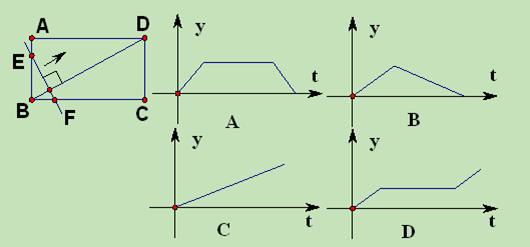
如图所示,在矩形ABCD中,垂直于对角线BD的直线  ,从点B开始沿着线段BD匀速平移到D.设直线
,从点B开始沿着线段BD匀速平移到D.设直线  被矩形所截线段EF的长度为y,运动时间为t,则y关于t的函数的大致图象是( )
被矩形所截线段EF的长度为y,运动时间为t,则y关于t的函数的大致图象是( )
某市打市电话的收费标准是:每次3分钟以内(含3分钟)收费 
元,以后每分钟收费  元(不足1分钟按1分钟计).某天小芳给同学打了一个6分钟的市
元(不足1分钟按1分钟计).某天小芳给同学打了一个6分钟的市
话,所用电话费为  元;小刚现准备给同学打市电话6分钟,他经过思考以后,决定先打
元;小刚现准备给同学打市电话6分钟,他经过思考以后,决定先打
3分钟,挂断后再打3分钟,这样只需电话费  元.如果你想给某同学打市话,准备通话
元.如果你想给某同学打市话,准备通话
10分钟,则你所需要的电话费至少为( )
 元
元
 元
元
 元
元
 元
元
对点(x,y )的一次操作变换记为P 1(x,y ),定义其变换法则
如下:P 1(x,y )=(  ,
,  );且规定
);且规定  (
(  为大于1的整数).如
为大于1的整数).如
P 1(1,2 )=(3,  ),P 2(1,2 )= P 1(P 1(1,2 ))= P 1(3,
),P 2(1,2 )= P 1(P 1(1,2 ))= P 1(3,  )=(2,4),P 3(1,
)=(2,4),P 3(1,
2 )= P 1(P 2(1,2 ))= P 1(2,4)=(6,  ).则P 2011(1,
).则P 2011(1,  )=( )
)=( )
| A. | (0,2 1005) | B. | (0,-2 1005) | C. | (0,-2 1006) | D. | (0,2 1006) |
在如图所示的正方形网格中,每个小正方形的边长
为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(  ,
,
5),(  ,3).
,3).
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.

为了解某县2011年初中毕业生的实验考查成绩等
级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成
绩绘制了如下的统计图表:
| 成绩等级 |
A |
B |
C |
D |
| 人数 |
60 |
x |
y |
10 |
| 百分比 |
30% |
50% |
15% |
m |

请根据以上统计图表提供的信息,解答下列问题:
⑴本次抽查的学生有___________________名;
⑵表中x,y和m所表示的数分别为:x=________,y=______,m=_________;
⑶请补全条形统计图;
⑷根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
如图,BD是□ABCD的对角线,∠ABD的平分线
BE交AD于点E,∠CDB的平分线  DF交BC于点F.
DF交BC于点F.
求证:△ABE≌△CDF.

某学校为开展"阳光体育"活动,计划拿出不超过
3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单
价比为8︰3︰2,且其单价和为130元.
⑴ 请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?
⑵ 若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球
数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?
如图,AB是半圆O的直径,点C是⊙O上一点
(不与A,B重合),连接AC,BC,过点O作OD∥AC交BC于点D,在OD的延长线上
取一点E,连接EB,使∠OEB=∠ABC.
⑴ 求证:BE是⊙O的切线;
⑵ 若OA=10,BC=16,求BE的长.

如图,已知二次函数  的图象经过
的图象经过
A(  ,
,  ),B(0,7)两点.
),B(0,7)两点.
⑴ 求该抛物线的解析式及对称轴;
⑵ 当  为何值时,
为何值时,  ?
?
⑶ 在  轴上方作平行于
轴上方作平行于  轴的直线
轴的直线  ,与抛物线交于C,D两点(点C在对称轴的左侧),
,与抛物线交于C,D两点(点C在对称轴的左侧),
过点C,D作  轴的垂线,垂足分别为F,E.当矩形CDEF为
轴的垂线,垂足分别为F,E.当矩形CDEF为  正方形时,求C点的坐标.
正方形时,求C点的坐标.

探究问题:
⑴方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB  与AD重合,由旋转可得:
与AD重合,由旋转可得:
AB="AD,BG=DE," ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF="45° " ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.

⑵方法迁移:
如图②,将  沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=  ∠DAB.试猜想DE,BF,EF之间有何数量
∠DAB.试猜想DE,BF,EF之间有何数量  关系,并证明你的猜想.
关系,并证明你的猜想.

⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足  ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).

“山东半岛蓝色经济区”规划主体区包括的海域面积共159500平方公里.159500用科学记数法表示为( )
| A.1595×102 | B.159.5×103 | C.15.95×104 | D.1.595×105 |
如图所示,在△ABC中,CD、BE分别是AB、AC边上的高,并且CD.BE相交于点P,若∠A=50°,则∠BPC等于
A.90° B.270° C.130° D.315°
为了了解某校2000名学生的体重情况,从中抽取了150名学生的体重,就这个问题来说,下面说法正确的是
| A.2000名学生的体重是总体 | B.2000名学生是总体 |
| C.每个学生是个体 | D.150名学生是所抽取的一个样本 |
设“○”、“口”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“口”、“△”这样的物体,按质量从小到大的顺序排列为 
| A.○△口 | B.○口△ | C.△口○ | D.口○△ |
点P(m+3,m+1)在直角坐标系中的x轴上,则点p坐标为
| A.(0,-2) | B.(2,0) | C.(4,0) | D.(0,一4) |
等腰三角形两边长分别为4,8,则它的周长为
| A.20 | B.16 | C.20或16 | D.不能确定 |
如果p(a-3,a+1)在第二象限,那么a的取值范围是
| A.a>-1 | B.a<3 | C.-3<a<3 | D.一1<a<3 |
某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为 人,组数为
人,组数为 组,则列方程组为
组,则列方程组为
A. |
B. |
C. |
D. |
用正三角形和正方形组合作平面镶嵌,每一个顶点周围有_______个正三角形和_______个正方形。
线段CD是由线段AB平移得到的。点A(-2,5)的对应点为C(3,7),则点B(-3,0)的对应点D的坐标为_______.
在平面直角坐标系中,点Q(-6,5)到x轴的距离是_______,到y轴的距离是_______。
某市为了了解七年级学生的身体素质情况,随机抽取了500名七年级学生进行检测,身体素质达标率为95%.请你估计该市7万名七年级学生中,身体素质达标的大约有_______万人.
已知△ABC的高为AD,∠BAD=70°,∠CAD=20°,则∠BAC的度数是_______。
(本小题满分8分)如图,EF∥AD,∠1=∠2,∠BAC=70°。求∠AGD.请将解题过程填写完整。
因为EF∥AD,(已知)
所以∠2=_________.( )
又因为∠1=∠2,(已知)
所以∠1=∠3.( )
所以AB//________.( )
所以∠BAC+_______=180°.( )
又因为∠BAC=70°,(已知)
所以∠AGD=________.
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 |
频数 |
百分比 |
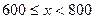 |
2 |
5% |
800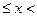 1000 1000 |
6 |
15% |
1000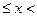 12000 12000 |
|
45% |
| |
9 |
22.5% |
| |
|
|
1600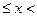 1800 1800 |
2 |
|
| 合计 |
40 |
100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
(本小题满分10分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积S△ABC.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A’B’C’,在图中画出△ABC变化位置,并写出△A’B’C’的坐标
 =________________.
=________________. =________.
=________.












 的正整数解有
的正整数解有
 ,用含
,用含 的代数式表示
的代数式表示 ,则
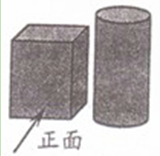
,则 的解集是_______.
的解集是_______.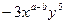 与单项式
与单项式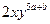 的和仍是单项式,则
的和仍是单项式,则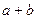 =_______.
=_______.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号