高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
下列四组函数中的f(x)与g(x)表示同一函数的有________.(填序号)
① f(x)=x0,g(x)= ;
;
② f(x)= ,g(x)=
,g(x)= ;
;
③ f(x)=x2,g(x)=( )4;
)4;
④ f(x)=|x|,g(x)=
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)=x2-2x,x∈[a,b]的值域为[-1,3],则b-a的取值范围是________.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
求下列函数的值域:
(1) y=x- ;
;
(2) y=x2-2x-3,x∈(-1,4];
(3) y= ,x∈[3,5];
,x∈[3,5];
(4) y= (x>1).
(x>1).
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
求下列函数的值域:
(1) f(x)= ;
;
(2) g(x)= ;
;
(3) y=log3x+logx3-1.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)=x2+4ax+2a+6.
(1) 若f(x)的值域是[0,+∞),求a的值;
(2) 若函数f(x)≥0恒成立,求g(a)=2-a|a-1|的值域.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)=1-2ax-a2x(a>1).
(1)求函数f(x)的值域;
(2)若x∈[-2,1]时,函数f(x)的最小值是-7,求a的值及函数f(x)的最大值.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为________.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)= 若a>b≥0,且f(a)=f(b),则bf(a)的取值范围是________.
若a>b≥0,且f(a)=f(b),则bf(a)的取值范围是________.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知二次函数f(x)=ax2-x+c(x∈R)的值域为[0,+∞),则 的最小值为________.
的最小值为________.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
已知函数f(x)= (-|x|+3)的定义域是[a,b](a、b∈Z),值域是[-1,0],则满足条件的整数对(a,b)有________对.
(-|x|+3)的定义域是[a,b](a、b∈Z),值域是[-1,0],则满足条件的整数对(a,b)有________对.
来源:2014届高考数学总复习考点引领+技巧点拨第二章第2课时练习卷
 的值域为____________.
的值域为____________.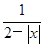 +lg(3x+1);
+lg(3x+1); .
. 的定义域;
的定义域; 的定义域.
的定义域. 的定义域为________.
的定义域为________. 的值域为________.
的值域为________. 则f(x)的值域是________.
则f(x)的值域是________. 粤公网安备 44130202000953号
粤公网安备 44130202000953号