高考数学全程总复习课时提升作业五十九第八章第十节练习卷
过抛物线y=2x2的焦点的直线与抛物线交于A(x1,y1),B(x2,y2),则x1x2=( )
| A.-2 | B.- |
C.-4 | D.- |
设M(x0,y0)为抛物线C:y2=8x上一点,F为抛物线C的焦点,若以F为圆心,|FM|为半径的圆和抛物线C的准线相交,则x0的取值范围是( )
| A.(2,+∞) | B.(4,+∞) |
| C.(0,2) | D.(0,4) |
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )
| A.1 | B. |
C.2 | D.2 |
若已知点Q(4,0)和抛物线y= x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )
A.2+2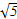 |
B.11 | C.1+2 |
D.6 |
已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为( )
A. +2 +2 |
B. +1 +1 |
C. -2 -2 |
D. -1 -1 |
若已知中心在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
| A.(0,+∞) | B.( ,+∞) ,+∞) |
C.( ,+∞) ,+∞) |
D.( ,+∞) ,+∞) |
设P为椭圆 +
+ =1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
设连接双曲线 -
- =1与
=1与 -
- =1(a>0,b>0)的4个顶点的四边形面积为S1,连接其4个焦点的四边形面积为S2,则
=1(a>0,b>0)的4个顶点的四边形面积为S1,连接其4个焦点的四边形面积为S2,则 的最大值为 .
的最大值为 .
过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0)作两直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时, 的值为 .
的值为 .
如图,已知椭圆C: +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且 ·
· =0.
=0.
(1)求椭圆C的方程.
(2)求证:直线l过定点,并求出该定点N的坐标.
已知椭圆E: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,a2与b2的等差中项为
,a2与b2的等差中项为 .
.
(1)求椭圆E的方程.
(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴相交于点P(t,0),求实数t的取值范围.
给定椭圆C: +
+ =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”的方程.
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.
①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;
②求证:|MN|为定值.
 +
+ =1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=
=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e= ,又椭圆经过点(
,又椭圆经过点( 粤公网安备 44130202000953号
粤公网安备 44130202000953号