广东省深圳市高三2月调研考试理科数学试卷
“ ”是“函数
”是“函数 在区间
在区间 上单调递减”的( )
上单调递减”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
执行如图所示的程序框图,则输出的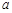 的值为( )
的值为( )
(注:“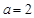 ”,即为“
”,即为“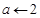 ”或为“
”或为“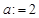 ”.)
”.)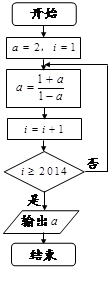
A.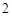 |
B.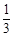 |
C. |
D.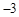 |
如图,在矩形 内:记抛物线
内:记抛物线 与直线
与直线 围成的区域为
围成的区域为 (图中阴影部分).随机往矩形
(图中阴影部分).随机往矩形 内投一点
内投一点 ,则点
,则点 落在区域
落在区域 内的概率是( )
内的概率是( )
A. |
B. |
C. |
D. |
在平面直角坐标系中,定义两点 与
与 之间的“直角距离”为
之间的“直角距离”为 .给出下列命题:
.给出下列命题:
(1)若 ,
, ,则
,则 的最大值为
的最大值为 ;
;
(2)若 是圆
是圆 上的任意两点,则
上的任意两点,则 的最大值为
的最大值为 ;
;
(3) 若 ,点
,点 为直线
为直线 上的动点,则
上的动点,则 的最小值为
的最小值为 .
.
其中为真命题的是( )
| A.(1)(2)(3) | B.(1)(2) | C.(1)(3) | D.(2)(3) |
某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是 .
在直角坐标系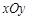 中,以原点
中,以原点 为极点,
为极点,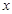 轴的正半轴为极轴建立极坐标系.若曲线
轴的正半轴为极轴建立极坐标系.若曲线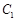 的参数方程为
的参数方程为 (
(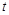 为参数),曲线
为参数),曲线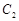 的极坐标方程为
的极坐标方程为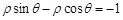 .则曲线
.则曲线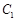 与曲线
与曲线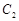 的交点个数为________个.
的交点个数为________个.
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):

若网购金额超过 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为 .
.
(1)试确定 ,
, ,
, ,
, 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)).
(2)该营销部门为了进一步了解这 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查.设
人进行问卷调查.设 为选取的
为选取的 人中“网购达人”的人数,求
人中“网购达人”的人数,求 的分布列和数学期望.
的分布列和数学期望.
如图,直线 ,抛物线
,抛物线 ,已知点
,已知点 在抛物线
在抛物线 上,且抛物线
上,且抛物线 上的点到直线
上的点到直线 的距离的最小值为
的距离的最小值为 .
.
(1)求直线 及抛物线
及抛物线 的方程;
的方程;
(2)过点 的任一直线(不经过点
的任一直线(不经过点 )与抛物线
)与抛物线 交于
交于 、
、 两点,直线
两点,直线 与直线
与直线 相交于点
相交于点 ,记直线
,记直线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
,  .问:是否存在实数
.问:是否存在实数 ,使得
,使得 ?若存在,试求出
?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 ,集合
,集合 ,集合
,集合 .则集合
.则集合 可表示为( )
可表示为( )



 满足
满足 (其中
(其中 为虚数单位),则
为虚数单位),则







 的展开式中常数项为( )
的展开式中常数项为( )



 的定义域为 .
的定义域为 . 与椭圆
与椭圆 有相同的焦点,且双曲线
有相同的焦点,且双曲线 的渐近线方程为
的渐近线方程为 ,则双曲线
,则双曲线 满足
满足 向量
向量 ,
, .若
.若 ,则实数
,则实数 的最大值为 .
的最大值为 . 中,已知
中,已知 ,
, ,且数列
,且数列 是等比数列,则
是等比数列,则 .
. 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 作弦
作弦 ,若
,若 ,
, ,则
,则 .
.
 的图像经过点
的图像经过点 .
. 的值;
的值; 中,
中, 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,若
,若 ,且
,且 .求
.求 .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. ,
, 的值;
的值; ;
; ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
. .
. 在
在 上的最大值;
上的最大值; 为曲线
为曲线 的切线,求实数
的切线,求实数 的值;
的值; 时,设
时,设 ,且
,且 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号