山东省德州市九年级第一学期期末考试数学试卷
平面直角坐标系内一点P(-2,3)关于原点对称点的坐标是( )
| A.(3,-2) | B.(2,3) | C.(-2,-3) | D.(2,-3) |
PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,则∠COD的度数是( )
| A.50° | B.60° | C.70° | D.75° |
已知OA平分∠BOC,P是OA上任意一点,如果以P为圆心的圆与OC相离,那么⊙P与OB的位置关系是( )
| A.相离 | B.相切 | C.相交 | D.不能确定 |
下列事件中是必然事件的是( )
| A.平移后的图形与原来图形对应线段相等。 |
| B.在一个等式两边同时除以同一个数,结果仍是等式。 |
| C.一个不透明的袋子中有6个红球1个黑球,每次摸出1个球然后放回搅匀,摸7次时一定会摸出一个黑球。 |
| D.任意一个五边形外角和等于540° |
如图,一张矩形报纸ABCD的长AB=a,宽BC=b,E,F分别是AB,CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比,则a:b等于( )
A. |
B. |
C. |
D. |
在直角坐标系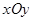 中,O是坐标原点,抛物线
中,O是坐标原点,抛物线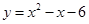 与x轴交与A,B两点(点A在点B的左侧),与y轴相交与点C,如果点M在y轴右侧的抛物线上,
与x轴交与A,B两点(点A在点B的左侧),与y轴相交与点C,如果点M在y轴右侧的抛物线上, ,那么点M的坐标是 。
,那么点M的坐标是 。
如图,铁道口栏杆的短臂长(OA)为1.25m,长臂长(OB)为16.5m,当短臂端点下降0.85m时,长臂端点升高了 。(不计杆的宽度)
长为1,宽为a的矩形纸片( ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为_____________.
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为_____________.
如图所示,在 △
△ 中,
中, ,
, ,将
,将 绕点
绕点 沿逆时针方向旋转
沿逆时针方向旋转 得到
得到 .
.
(1)线段 的长是 ,
的长是 , 的度数是 ;
的度数是 ;
(2)连接 ,求证:四边形
,求证:四边形 是平行四边形.
是平行四边形.
随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2012年为10万只,预计2014年将达到14.4万只。求该地区2012年到2014年高效节能灯年销售量的平均增长率。
已知:如图所示,AB是⊙ 的弦,
的弦, ,C是优弧AB上的一点,BD//OA,交CA的延长线于点D,连接BC。
,C是优弧AB上的一点,BD//OA,交CA的延长线于点D,连接BC。
(1)求证:BD是⊙ 的切线;
的切线;
(2)若 ,求⊙
,求⊙ 的半径。
的半径。
小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字3、4、5,现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.如果和为奇数,则小明胜;和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为8的概率;
(2)你认为这个游戏对双方公平吗?说说你的理由.
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y= 的图像经过B、C两点.
的图像经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图像探索:当y>0时x的取值范围.







 向左平移2个单位,再向下平移3个单位,得到的抛物线是( )
向左平移2个单位,再向下平移3个单位,得到的抛物线是( )

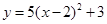

 。
。 吨化肥,以后每季度比上一季度增产
吨化肥,以后每季度比上一季度增产 %,则第三季度化肥增产的吨数为 。
%,则第三季度化肥增产的吨数为 。 ,则抽到女生的概率是 。
,则抽到女生的概率是 。 (2)
(2)
 的方程
的方程 的一个根是另一个根的2倍,求
的一个根是另一个根的2倍,求 的值.
的值. ),那么:
),那么:
 ,求
,求 的函数解析式。
的函数解析式。 粤公网安备 44130202000953号
粤公网安备 44130202000953号