浙江省杭州市长河高三市二测模考数学文卷
已知条件p: ;条件q:
;条件q: ,若p是q的充分不必要
,若p是q的充分不必要 条件,则m的取值范围是 ( )
条件,则m的取值范围是 ( )
| A.[21,+∞] | B.[9,+∞] | C.[19,+∞] | D.(0,+∞) |
如图,在棱长相等的四面体S-ABC中,
E、F分别是SC、AB的中点,
则直线EF与SA所成的角为( )
A.90° B.60°
C.45° D.30°
已知 表示直线,
表示直线, 表示平面,下列条件中能推出结论的正确的是 ( )
表示平面,下列条件中能推出结论的正确的是 ( )
条件:① ,
,  ,
,  ; ②
; ② ∥
∥ ,
,  ∥
∥ ; ③
; ③ ,
,  ∥
∥ ;④
;④  ,
,  ⊥
⊥ 。结论:a:
。结论:a:  b:
b:  ⊥
⊥ c:
c:  ∥
∥ d:
d:  ∥
∥
A.① a,② a,② b,③ b,③ c,④ c,④ d d |
B.① b,② b,② d,③ d,③ a,④ a,④ c c |
C.① c,② c,② d,③ d,③ a,④ a,④ b b |
D.① d,② d,② b,③ b,③ a,④ a,④ c c |
已知非零向量 和
和 满足
满足 ,且
,且 ,
,
则△ABC为 ( )
| A.等边三角形 | B.等腰非直角三角形 |
| C.非等腰三角形 | D.等腰直角三角形 |
.设直角三角形的两直角边的长分别为 ,斜边长为
,斜边长为 ,斜边上的高为
,斜边上的高为 ,则有
,则有 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论:
① ;②
;② ;③
;③  ;④
;④ .
.
其中正确结论的序号是 ;进一步得到的一般结论是 .
(本小题满分14分)在△ABC中, 分别为角A、B、C的对边,
分别为角A、B、C的对边, ,
,  ="3," △ABC的面积为6.
="3," △ABC的面积为6.
⑴ 角A的正弦值; ⑵求边 b、c.
b、c. 
.(本小题满分14分)
已知单调递增的等比数列 满足:
满足: ;
;
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列 的前n项和为
的前n项和为 ,求
,求 成立的正整数 n的最小值.
成立的正整数 n的最小值.
(本小题满分14分)
如图所示, 平面
平面 ,底面
,底面 为菱形,
为菱形, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: //平面
//平面 ;
;
(3) 求二面角 的平面角的大小.
的平面角的大小.
(本小题满分15分)
设函数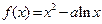 与
与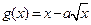 的图像分别交直线
的图像分别交直线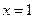 于点
于点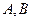 ,且曲线
,且曲线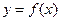 在点
在点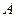 处的切线与曲线
处的切线与曲线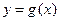 在点
在点 处的切线平行.
处的切线平行.
(1)求函数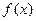 ,
, 的表达式;
的表达式;
(2)设函数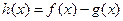 ,求函数
,求函数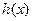 的最小值;
的最小值;
(3)若不等式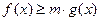 在
在 上恒成立,求实数
上恒成立,求实数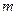 的取值范围.
的取值范围.
 的虚部为 ( )
的虚部为 ( )



 的图象,则图2中的图象对应的函数可能是( )
的图象,则图2中的图象对应的函数可能是( )




 的前5项之和
的前5项之和 ,且
,且 ,则
,则 ( )
( ) ,则
,则 的值是 ( )
的值是 ( )








 与直线
与直线 有两个交点时,实数k的取值范围是( )
有两个交点时,实数k的取值范围是( )



 是等比数列,对
是等比数列,对 恒成立,且
恒成立,且 ,
, 等于 .
等于 .  满足
满足 ,
, 满足
满足 ,则
,则 非等腰直角三角形的概率是 .
非等腰直角三角形的概率是 . 左支上一点,
左支上一点, 为双曲线的左右焦点,且
为双曲线的左右焦点,且  则此双曲线离心率是 .
则此双曲线离心率是 . 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为  上是增函数,且
上是增函数,且 对所有的
对所有的 ,
, 都成立,则t的取值范围是________________.
都成立,则t的取值范围是________________. 5分)
5分) 的斜率为
的斜率为 且过点
且过点 ,抛物线
,抛物线
 , 直线与抛物线
, 直线与抛物线 是抛物线的焦点,点
是抛物线的焦点,点 为抛物线内一定点,点
为抛物线内一定点,点 为抛物线上一动点.
为抛物线上一动点. 的最小值;
的最小值; 为坐标原点,问是否存在点
为坐标原点,问是否存在点 ,使过点
,使过点 两点,且以
两点,且以 为直径的圆恰过坐标原点, 若存在,求出动点
为直径的圆恰过坐标原点, 若存在,求出动点 粤公网安备 44130202000953号
粤公网安备 44130202000953号