辽宁省瓦房店市五校高二上学期竞赛数学理卷
设集合S={x|x2-5|x|+6="0}," T={x|(a-2)x="2}," 则满足T (≠S的a的值共有 ( )
| A.5 | B.4 | C.3 | D.2 |
已知 =(cos
=(cos π, sin
π, sin π),
π),  ,
,  ,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
| A.1 | B. |
C.2 | D. |
已知定义在R上的函数 满足下列三个条件:
满足下列三个条件:
①对任意的x∈R都有 ;
;
②对于任意的 ,都有
,都有
③ 的图象关于y轴对称. 则下列结论中正确的是 ( )
的图象关于y轴对称. 则下列结论中正确的是 ( )
A. |
B. |
C. |
D. |
若f(x)=|lgx|,当a<b<c时,f(a)>f(c)>f(b).则下列不等式中正确的为( )。
| A.(a-1)(c-1)>0 | B.ac>1 | C.ac=1 | D.ac<1 |
.函数 是定义在R上恒不为0的函数,对任意
是定义在R上恒不为0的函数,对任意 都有
都有 ,
,
若 ,则数列
,则数列 的前n项和Sn的取值范围是
的前n项和Sn的取值范围是 ( )
( )
A. |
B. |
C. |
D.  |
函数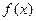 的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有
的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有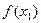 ≤
≤ ,
,
则称函数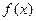 在D上为非减函数.设函数
在D上为非减函数.设函数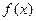 在[0,1]上为非减函数,且满足以下三个条件:①
在[0,1]上为非减函数,且满足以下三个条件:①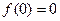 ;②
;②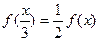 ③
③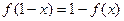
则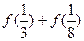 +
+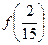 等于 ( )
等于 ( )
A.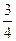 |
B.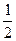 |
C.1 | D.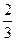 |
关于函数 有下列命题:
有下列命题:
①函数 的图象关于y轴对称 ②在
的图象关于y轴对称 ②在 上
上 是增函数;在
是增函数;在 上
上 是减函数 ③函数
是减函数 ③函数 的最小值是
的最小值是 ④在
④在 上
上 为增函数
为增函数
⑤ 无最大值,也无最小值 ,其中正确命题的序号是_________
无最大值,也无最小值 ,其中正确命题的序号是_________
.设有一组圆 .下列四个命题:
.下列四个命题:
| A.存在一条定直线与所有的圆均相切 |
| B.存在一条定直线与所有的圆均相交 |
| C.存在一条定直线与所有的圆均不相交 |
| D.所有的圆均不经过原点 |
其中真命题的代号是 .(写出所有真命题的代号)
(本小题满分10分)已知函数 ,
, .
.
(1)求 的最大值和最小值;
的最大值和最小值;
(2)若不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
.(本小题满分12分)如图,在正方体 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)如果 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱 、
、 、
、 、
、 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
.已知椭圆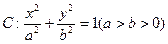 过点
过点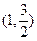 ,且离心率e=.
,且离心率e=.
(1)求椭圆方程;
(2)若直线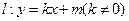 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、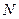 ,且线段
,且线段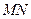 的垂直平分线过定点
的垂直平分线过定点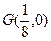 ,求
,求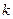 的取值范围。
的取值范围。
.(本小题满分12分)设函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
(1)求 的值;
的值;
(2)若不等式 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值.
 的直线
的直线 将圆
将圆 分成两段弧,当其中的优弧最长时,
分成两段弧,当其中的优弧最长时,



 的图象如右图所示,则函数
的图象如右图所示,则函数 的单调递减区间是( )
的单调递减区间是( )




 则函数
则函数 的最大值为( )
的最大值为( ) 为奇函数, 且在[0,
为奇函数, 且在[0, ]为增函数, 则
]为增函数, 则 的一个值为( )
的一个值为( )



 、
、 、
、 、
、 是半径为
是半径为 的球面上的四点,且满足
的球面上的四点,且满足 ,
, ,
, ,则
,则 的最大值是 ( )
的最大值是 ( )



 ,满足
,满足 时有
时有 恒成立,且
恒成立,且
 与
与 的大小为 ( )
的大小为 ( )


 大小不定
大小不定 , 若
, 若 的最大值为
的最大值为 , 最小值为
, 最小值为 , 则
, 则
 上不存在关于直线
上不存在关于直线 对称的两点,则
对称的两点,则 的取值范围是
的取值范围是  .若
.若 为整数,且函数
为整数,且函数 在
在 内恰有一个零点,求
内恰有一个零点,求 ,若
,若 ,则称
,则称 为
为 ,则称
,则称 和
和 ,即
,即 ,
, .
. ;
; ,且
,且 ,求实数
,求实数 的取值范围;
的取值范围;  上的单调递增函数,
上的单调递增函数, 是函数的稳定点,问
是函数的稳定点,问 粤公网安备 44130202000953号
粤公网安备 44130202000953号