2011年初中毕业升学考试（湖南郴州卷）数学

某工厂有一种材料，可加工甲、乙、丙三种型号机械配件共240件，厂方计划由20个工人一天内加工完成，并要求每人只加工一种配件，根据下表提供的信息，解答下列问题：

（1）设加工甲种配件的人数为x，加工乙种配件的人数为y，求y与x之间的函数关系式
（2）如果加工每种配件的人数均不少于3人，那么加工配件的人数安排方案有几种？并写出每种安排方案
（3）要使此次加工配件的利润最大，应采用哪种方案？最大利润是多少？

如图①，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起
（1）操作：如图②，将△ECF的顶点F固定在△ABD的BD边上的中点处，将△ECF绕点F在BD的上方左右旋转，设旋转时FC交BA于H（不与点B重合），EF交DA于G（不与点D重合），求证：BH·GD=BF²
（2）操作：如图③，△ECF的顶点F在△ABD的BD边上滑动（不与点B、D重合），且CF如终过点A，过点A作AG∥CE，交EF于G，连接DG
探究：FD+DG=      ，并请证明你的结论

九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践——应用——探究的过程
（1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量，测得隧道的路面宽为10米，隧道顶部最高处距地面6.25米，并画出了隧道截面图，建立了如图所示的直角坐标系，请你求出抛物线的解析式
（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖起方向上的高度差至少为0.5米，为了确保安全，问该隧道能否让最宽3米，最高3.5米的两辆车居中并列行驶（不考虑两车之间的空隙）？
（3）探究：该课题学习小组为进一步探究抛物线的有关知识，他们借助上述抛物线模型，提出了以下两个问题，请予解答：
①如图，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上，设矩形ABCD的周长为为l，求l的最大值
②如图，过原点作一条直线y=x，交抛物线于M，交抛物线的对称轴于N，P为直线OM上一动点，过点P作x轴的垂线交抛物线于点Q，问在直线OM上是否存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由

（11·台州）下列四个几何体中，主视图是三角形的是【   】

（11·台州）要反映台州市某一周每天的最高气温的变化趋势，宜采用【   】

（11·台州）计算(a³)²的结果是【   】

（11·台州）若两个相似三角形的面积之比为1∶4，则它们的周长之比为【   】

（11·台州）在梯形ABCD中，AD∥BC，∠ABC＝90º，对角线AC、BD相交于
点O．下列条件中，不能判断对角线互相垂直的是【   】
A．∠1＝∠2          B．∠1＝∠3
C．∠2＝∠3          D．OB²＋OC²＝BC²

（11·台州）如图是一个组合烟花的横截面，其中16个圆的半径相同，点A、B、
C、D分别是四个角上的圆的圆心，且四边形ABCD为正方形．若圆的半径为r，组合烟花
的高为h，则组合烟花侧面包装纸的面积至少需要(接缝面积不计)【   】
A．                  B．
C．             D．

（11·台州）如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l
上的一个动点，PQ切⊙O于点Q，则PQ的最小值为【   】

A．

B．

C．3

D．2

（11·台州）若二次根式有意义，则x的取值范围是         ．

（11·台州）袋子中装有2个黑球和3个白球，这些球的形状、大小、质地等完
全相同．随机地从袋子中摸出一个白球的概率是      ．

因式分解：a²＋2a＋1＝

（11·台州）点D、E分别在等边△ABC的边AB、BC上，将△BDE沿直线DE
翻折，使点B落在B₁处，DB₁、EB₁分别交边AC于点F、G．若∠ADF＝80º，则∠CGE
＝         ．

（11·台州）如果点P(x，y)的坐标满足x＋y＝xy，那么称点P为和谐点．
请写出一个和谐点的坐标：           ．

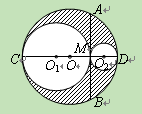
（11·台州）如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB＝20，分
别以CM、DM为直径作两个大小不同的⊙O₁和⊙O₂，则图中阴影部分的面积为       (结
果保留)．

（11·台州）(8分)计算：．

（11·台州）(8分)如图，分别延长□ABCD的边BA、DC到点E、H，使得AE
＝AB，CH＝CD，连接EH，分别交AD、BC于点F、G．
求证：△AEF≌△CHG．

（11·台州）(8分)毕业在即，九年级某班为纪念师生情谊，班委决定花800元
班费买两种不同单价的留念册，分别给50位同学和10位任课教师每人一本作纪念，其中送
给任课教师的留念册单价比给同学的单价多8元．请问这两种不同留念册的单价分别是多
少？

（11·台州）(10分)丁丁想在一个矩形材料中剪出如图阴影所示的梯形，作为要制作的风筝的一个翅膀．请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位，≈1.7)．

（11·台州）(12分)2011年5月19日，中国首个旅游日正式启动．某校组织了
八年级800名学生参加的旅游地理知识竞赛，李老师为了了解学生对旅游地理知识的掌握情
况，从中随机抽取了部分学生的成绩作为样本，把成绩按优秀、良好、及格和不及格4个级
别进行统计，并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出)．

请根据以上提供的信息，解答下列问题：
(1)求被抽取部分学生的人数；
(2)请补全条形统计图，并求出扇形统计图中表示及格的扇形的圆心角度数；
(3)请估计八年级800名学生中达到良好和优秀的总人数．

（11·台州）(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，
点D是垂足，点E是BC的中点，规定：．特别地，当点D、E重合时，规定：λ_A
＝0．另外，对λ_B、λ_C作类似的规定．

(1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λ_A、λ_C；
(2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λ_A＝2，面积也为2；
(3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：
①若△ABC中λ_A＜1，则△ABC为锐角三角形；【   】
②若△ABC中λ_A＝1，则△ABC为锐角三角形；【   】
③若△ABC中λ_A＞1，则△ABC为锐角三角形．【   】

任意写出一对互为倒数的数：________ 和 _______.

某班有女生a人，男生比女生的2倍少5人，则男生有___________________人.

不等式组 的解集是__________.

如图1，在要使,则需增加条件_____________（限写一个）.                                 

如图2，A、B两点位于一个池塘的两端，冬冬想用绳子测量A、B两点间的距离，但绳子不够长，一位同学帮他想了一个办法：先在地上取一个可以直接到达A、B的点C，找到AC，BC的中点D、E，并且测得DE的长为15m，则A、B两点间的距离为__________.
 图2

下列各数：、、、、0.01020304…中是无理数的
有_____________________.

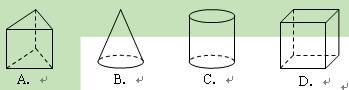
一个圆锥形的蛋筒，底面圆直径为7cm，母线长为14cm，把它的包
装纸展开，侧面展开图的面积为__________________cm²(不计折叠部分).

如图3，四边形ABCD是O的内接四边形，∠DCE＝，则            

∠BAD＝______________.                                                

－4的绝对值是                                              （     ）
A. 4             B.             C. －4             D.  

函数中，自变量x的取值范围是                       (       )
A. x < 1           B. x ≤ 1        C. x > 1             D. x≥1     

下列运算中
(1)          (2)           (3)
(4)      (5)
其中正确的运算有                                                   (      )
A. 1个          B. 2个               C. 3个              D. 4个

A.          B.                  C.                D.

下列图案中不是中心对称图形的是                                     （    ）
 

 

下面式子从左边到右边的变形中是因式分解的是                         （    ）
A.              B.          
C.               D.

方程的左边配成完全平方后所得方程为                   （    ）
A.     B.      C.    D. 以上答案都不对

在一个四边形ABCD中，依次连结各边中点的四边形是菱形，则对角线AC与BD需要满足条件                                                            （    ）
A. 垂直          B. 相等             C.垂直且相等      D. 不再需要条件

下列命题中，正确的命题是                                           （    ）
A. 有两条边和其中一条边所对的角相等的两个三角形是全等三角形
B. 相似三角形面积之比等于相似比
C. 任意多边形的外角和都等于
D. 过切点的直线是圆的切线

一个正常人在做激烈运动时，心跳速度加快，当运动停止下来后，心跳次数N(次)与时间s(分)的函数关系图像大致是  （     ）





                                            
 
 
A                   B                  C                 D

计算：

某中学在一次法律知识测试中，抽取部分学生成绩（分数为整
数，满分100分）将所得得数据整理后，画出频率分布直方图，已
知图中从左到右的三个小组的频率分别为0.04，0.06，0.82，第二
小组的频数为3.
(1)本次测试中抽样的学生有多少人？
(2)分数在90.5～100.5这一组的频率是多少？有多少人？                   
(3)若这次成绩在80分以上（含80分）为优秀，则优秀率不低于多少？
                                                                     

如图7，有两棵树，一棵高10米，另一棵高4米，两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？

		图7

证明题24．如图8，在  ABCD中，DE＝BF.

求证：四边形AFCE是平行四边形.

今年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同.
（1）求降低的百分率；
（2）若小红家有4人，明年小红家减少多少农业税？
（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税.

已知：如图9，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6），且AB＝.

（1）求点B的坐标；
（2）求经过A、B、D三点的抛物线的解析式；
（3）在（2）中所求的抛物线上是否存在一点P，

使得?若存在，请求出该点坐标，