[河南]2013-2014学年河南郑州高二上学期期末考试文科数学试卷
若 ,则
,则 是
是 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知抛物线 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )
| A.5 | B.6 | C.7 | D.8 |
已知函数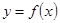 的导函数
的导函数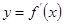 的图象如图所示,则关于函数
的图象如图所示,则关于函数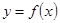 ,下列说法正确的是 ( )
,下列说法正确的是 ( )
A.在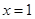 处取得最大值 处取得最大值 |
B.在区间 上是增函数 上是增函数 |
C.在区间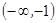 上函数值均小于0 上函数值均小于0 |
D.在 处取得极大值 处取得极大值 |
设等差数列 的公差
的公差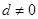 ,
,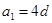 ,若
,若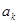 是
是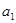 与
与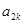 的等比中项,则
的等比中项,则 =( )
=( )
| A.3或6 | B.3 或9 | C.3 | D.6 |
要做一个圆锥形的漏斗,其母线长为10,要使其体积最大,则高应为( )
A. |
B.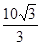 |
C.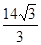 |
D.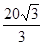 |
已知等差数列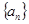 的通项公式为
的通项公式为 ,设
,设 ,则当
,则当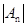 取得最小值是,n的值是( )
取得最小值是,n的值是( )
| A.17 | B.16 | C.15 | D.13 |
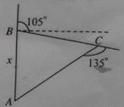
如图一蜘蛛从A点出发沿正北方向爬行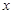 cm到B处捉到一只小虫,然后向右转
cm到B处捉到一只小虫,然后向右转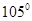 ,爬行10cm到C处捉到另一只小虫,这时它向右转
,爬行10cm到C处捉到另一只小虫,这时它向右转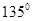 爬行回到它的出发点,那么
爬行回到它的出发点,那么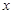 = .
= .
已知命题:①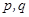 为两个命题,则“
为两个命题,则“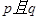 为真”是“
为真”是“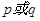 为真”的必要不充分条件;②若
为真”的必要不充分条件;②若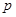 为:
为: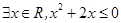 ,则
,则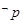 为:
为: ;③命题
;③命题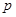 为真命题,命题
为真命题,命题 为假命题,则命题
为假命题,则命题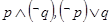 都是真命题;④命题“若
都是真命题;④命题“若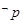 ,则
,则 ”的逆命题是“若
”的逆命题是“若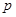 ,则
,则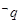 ”。期中正确命题的序号是 .
”。期中正确命题的序号是 .
已知命题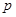 :“不等式
:“不等式 对任意
对任意 恒成立”,命题
恒成立”,命题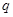 :“
:“ 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若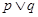 为真命题,
为真命题,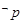 为真,求实数
为真,求实数 的取值范围.
的取值范围.
在 中,
中, 分别是角A,B,C的对边,且满足
分别是角A,B,C的对边,且满足 .
.
(1)求角B的大小;
(2)若 最大边的边长为
最大边的边长为 ,且
,且 ,求最小边长.
,求最小边长.
某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用 表示,且
表示,且 (其中
(其中 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?
已知椭圆C: 的左、右焦点和短轴的一个端点构成边长为4的正三角形.
的左、右焦点和短轴的一个端点构成边长为4的正三角形.
(1)求椭圆C的方程;
(2)过右焦点 的直线
的直线 与椭圆C相交于A、B两点,若
与椭圆C相交于A、B两点,若 ,求直线
,求直线 的方程.
的方程.
 的图象上一点(0,1)处的切线的斜率为( )
的图象上一点(0,1)处的切线的斜率为( ) 都是等差数列,若
都是等差数列,若 则
则 ( )
( )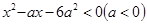 的解集为( )
的解集为( )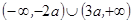
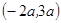
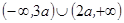

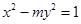 的一个焦点坐标为
的一个焦点坐标为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
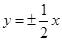
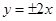

 满足
满足 则目标函数
则目标函数 的最小值为( )
的最小值为( )
 中,
中,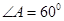 ,AB=2,且
,AB=2,且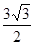 ,则BC的长为( )
,则BC的长为( )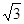
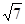
 为等比数列,
为等比数列,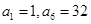 ,则
,则 .
.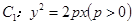 的焦点F恰好是双曲线
的焦点F恰好是双曲线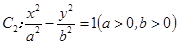 的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 .
的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 . ,
, ,且满足
,且满足 .
. 是等差数列;
是等差数列; ,求数列
,求数列 的前n项和
的前n项和 .
. 的图象在点
的图象在点 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1. 的值;
的值; 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号