[广东]2014届广东珠海高三上学期期末学生学业质量监测文数学卷
学校为了解学生课外读物方面的支出情况,抽取了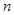 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在 (单位:元),其中支出在
(单位:元),其中支出在 (单位:元)的同学有
(单位:元)的同学有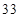 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )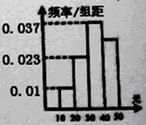
A. |
B. |
C. |
D.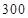 |
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
对定义域为 的函数,若存在距离为
的函数,若存在距离为 的两条平行直线
的两条平行直线 和
和 ,使得当
,使得当 时,
时, 恒成立,则称函数
恒成立,则称函数 在
在 有一个宽度为
有一个宽度为 的通道.有下列函数:①
的通道.有下列函数:① ;②
;② ;③
;③ ;④
;④ .其中在
.其中在 上通道宽度为
上通道宽度为 的函数是( )
的函数是( )
| A.①③ | B.②③ | C.②④ | D.①④ |
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
已知在平面直角坐标系 中圆
中圆 的参数方程为:
的参数方程为: ,(
,( 为参数),以
为参数),以 为极轴建立极坐标系,直线极坐标方程为:
为极轴建立极坐标系,直线极坐标方程为: ,则圆
,则圆 截直线所得弦长为 .
截直线所得弦长为 .
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的 名候车乘客中随机抽取
名候车乘客中随机抽取 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 |
候车时间 |
人数 |
| 一 |
 |
 |
| 二 |
 |
 |
| 三 |
 |
 |
| 四 |
 |
 |
| 五 |
 |
 |
(1)求这 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
如图,在三棱柱 中,四边形
中,四边形 为菱形,
为菱形,
 ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: 面
面 ;
;
(3)求三棱锥 的体积.
的体积.
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
已知数列 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有
 ,其中
,其中 为数列
为数列 的前
的前 项和.
项和.
(1)求 、
、 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,对任意的
,对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
来源:2014届广东珠海高三上学期期末学生学业质量监测文数学卷
 ,集合
,集合 ,
, ,则
,则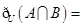 ( )
( )
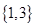


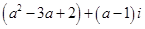 是纯虚数,则实数
是纯虚数,则实数 的值为( )
的值为( )


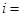 ( )
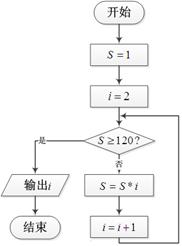
( )




 、
、 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( )



 中,
中, ,则
,则 等于( )
等于( )








 共有奇数项,所有奇数项和
共有奇数项,所有奇数项和 ,所有偶数项和
,所有偶数项和 ,末项是
,末项是 ,则首项
,则首项 ( )
( )



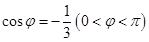 ,则
,则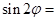 ( )
( )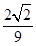

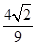
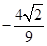
 、
、 满足线性约束条件
满足线性约束条件 ,则目标函数
,则目标函数 的最大值为 .
的最大值为 . 在点
在点 处的切线方程为 .
处的切线方程为 . 上的函数
上的函数 满足
满足 ,则
,则 .
. 是圆
是圆 的直径,
的直径, 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 平行于弦
平行于弦 ,若
,若 ,
, ,则
,则 .
.
 ,
, .
. 的值;
的值; 时,求
时,求 的最值.
的最值. ,
, .
. 的极值点;
的极值点; ,记
,记 上的最小值为
上的最小值为 ,求
,求 的最小值.
的最小值. 的左、右焦点分别为
的左、右焦点分别为 、
、 ,
, 为原点.
为原点. 为椭圆
为椭圆 上的一点,
上的一点, 是
是 的中点,且
的中点,且 ,求点
,求点 轴的距离;
轴的距离;
 与椭圆
与椭圆 、
、 两点,若在椭圆
两点,若在椭圆 ,使四边形
,使四边形 为平行四边形,求
为平行四边形,求 的取值范围.
的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号