上海市浦东新区高三第一学期质量抽测数学理卷
从一个底面半径和高都是 的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.
的圆柱中,挖去一个以圆柱的上底为底,下底面的中心为顶点的圆锥,得到一个如图(1)所示的几何体,那么这个几何体的体积是_________________.
世博期间,5人去某地铁站参加志愿者活动,该地铁站有4个出口,要求每个出口都要有志愿者服务,不同安排方法有__________________种(用数值表示).
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
| 时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
| 10∶00 |
9.5 |
300 |
| 11∶00 |
9.6 |
220 |
注:油耗= ,可继续行驶距离=
,可继续行驶距离= ,
,
平均油耗 .
.
从上述信息可以推断在10∶00—11∶00这1小时内________ (填上所有正确判断的序号) .
向前行驶的里程为80公里;
向前行驶的里程不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
⑤ 平均车速超过80公里/小时.
关于数列{an}有以下命题,其中错误的命题为 ( )
A.若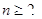 且 且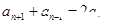 ,则 ,则 是等差数列 是等差数列 |
B.设数列 的前 的前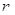 项和为 项和为 ,且 ,且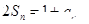 ,则数列 ,则数列 的通项 的通项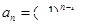 |
C.若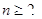 且 且 ,则 ,则 是等比数列 是等比数列 |
D.若 是等比数列,且 是等比数列,且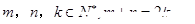 ,则 ,则 |
点O在 所在平面内,给出下列关系式:
所在平面内,给出下列关系式:
(1) ;
;
(2) ;
;
(3) ;
;
(4) .
.
则点O依次为 的( )
的( )
| A.内心、外心、重心、垂心 | B.重心、外心、内心、垂心 |
| C.重心、垂心、内心、外心 | D.外心、内心、垂心、重心 |
(本小题满分14分,第1小题满分6分,第2小题满分8分)
已知向量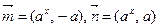 ,其中
,其中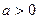 且
且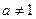 ,
,
(1)当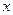 为何值时,
为何值时, ;
;
(2)解关于x的不等式 .
.
(本小题满分14分,第1小题满分6分,第2小题满分8分)
野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架 (如图3)进行野炊训练. 已知
(如图3)进行野炊训练. 已知 ,
, 、
、 两点间距离为
两点间距离为 .
.
(1)求斜杆 与地面
与地面 所成角的大小(用反三角函
所成角的大小(用反三角函 数值表示)
数值表示) ;
;
(2)将炊事锅看作一个点 ,用吊绳
,用吊绳 将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅
将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅 到地面
到地面 及各条斜杆的距离都不小于30
及各条斜杆的距离都不小于30 ,试问吊绳
,试问吊绳 长的取值范围.
长的取值范围.
(本小题满分16分,第1小题满分6分,第2小题满分10分)
已知
(1)  时,求
时,求 的值域;
的值域;
(2)  时,
时, 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: ,求b的取值范围.
,求b的取值范围.
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的 ,总有
,总有 成立,求常数
成立,求常数 的值;
的值;
(2)在数列 中,
中, ,
, (
( ,
, ),求通项
),求通项 ;
;
(3)在(2)题的条件下,设 ,从数列
,从数列 中依次取出第
中依次取出第 项,第
项,第 项,…第
项,…第 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列 ,其中
,其中 ,其中
,其中 ,
, .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数 的值;不存在,说明理由.
的值;不存在,说明理由.
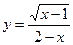 的定义域为__________________.
的定义域为__________________.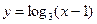 的反函数是__________________.
的反函数是__________________.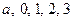 的平均数为1,则这五个数的方差等于__________________.
的平均数为1,则这五个数的方差等于__________________. 的解为__________________.
的解为__________________.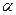 :
: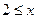
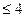 ”是“条件
”是“条件 :
: ”的充分条件,则
”的充分条件,则 的取值范围是__________________.
的取值范围是__________________. 中,
中, ,则数列
,则数列 中,
中, ,则
,则 的长等于__________________.
的长等于__________________. ,则
,则 的取值范围是___________
的取值范围是___________ _______.
_______. ,则输出
,则输出 的值为__________________.
的值为__________________.
 有实数根
有实数根 ,则复数
,则复数 __________________.
__________________. 上的函数
上的函数 ,
, ,
, __________________
__________________ 是偶函数,则
是偶函数,则 可取的一个值为( )
可取的一个值为( )



 、
、 ,使复数
,使复数 为实数的概率是 ( )
为实数的概率是 ( )



 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 是否是“S-函数”;
是否是“S-函数”; 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
; 的函数
的函数 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和 ,当
,当 时,
时, ,求当
,求当 时函数
时函数 粤公网安备 44130202000953号
粤公网安备 44130202000953号