[天津]2014届天津学大教育信息咨询有限公司九年级上学期期末复习数学卷
已知二次函数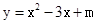 (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程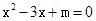 的两实数根是
的两实数根是
| A.x1=1,x2=-2 | B.x1=1,x2=2 | C.x1=1,x2=0 | D.x1=1,x2=3 |
已知二次函数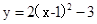 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.y有最小值0,有最大值-3 |
| B.y有最小值-3,无最大值 |
| C.y有最小值-1,有最大值-3 |
| D.y有最小值-3,有最大值0 |
已知两个半径不相等的圆外切,圆心距为,大圆半径是小圆半径的倍,则小圆半径为
A.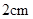 或 或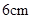 |
B.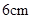 |
C.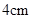 |
D.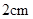 |
已知二次函数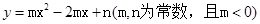 ,下列自变量取值范围中y随x增大而增大的是( ).
,下列自变量取值范围中y随x增大而增大的是( ).
| A.x<2 | B.x<-1 | C.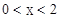 |
D.x>-1 |
如图,抛物线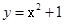 与双曲线
与双曲线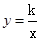 的交点A的横坐标是1,则关于
的交点A的横坐标是1,则关于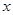 的不等式
的不等式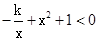 的解集是( )
的解集是( )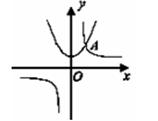
| A.x>1 | B.x<1 | C.0<x<1 | D.-1<x<0 |
假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是
A.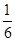 |
B.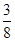 |
C.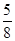 |
D.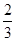 |
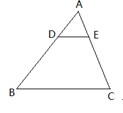
如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A.BD⊥AC B.AC2=2AB·AE
C.BC=2AD D.△ADE是等腰三角形
如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是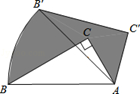
A.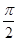 |
B.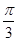 |
C.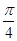 |
D. |
二次函数y=ax2+bx+c的图象如图所示,有下列结论:
①a<0,②b<0,③c<0,④4a-2b+c<0,⑤b+2a=0
其中正确的个数有( )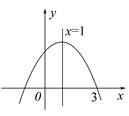
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .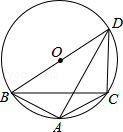
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+x+,则该运动员此次掷铅球,铅球出手时的高度为 .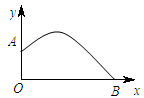
如图,⊙M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,圆心M的坐标为 .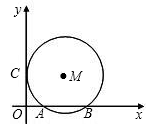
为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 米.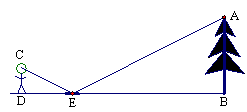
如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2,则正八边形的面积为 cm2.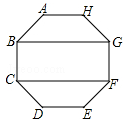
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.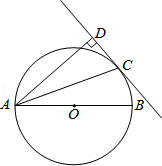
(1)求证:AC平分∠BAD;
(2)若CD=1,AC=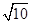 ,求⊙O的半径长.
,求⊙O的半径长.
已知抛物线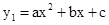 (a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
(a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
| x |
… |
―1 |
0 |
3 |
… |
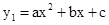 |
… |
0 |
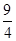 |
0 |
… |
(1)求y1与x之间的函数关系式;
(2)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记P(x,y2).
①求y2与x之间的函数关系式;
②当x取任意实数时,若对于同一个x,有y1<y2恒成立,求t的取值范围.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表表示:
| 等级(x级) |
一级 |
二级 |
三级 |
… |
| 生产量(y台/天) |
78 |
76 |
74 |
… |
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出与之间的函数关系式:_____;
(2)每台护眼灯可获利z(元)关于等级x(级)的函数关系式:______;
(3)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.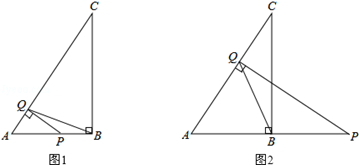
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.
(1)求直线AB的解析式;
(2)当点P运动到点(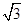 ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;
(3)是否存在点P,使△OPD的面积等于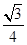 ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号