[福建]2014届福建四地六校高三上学期第三次月考理科数学试卷
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.既不充分也不必要条件 |
| C.充要条件 | D.必要不充分条件 |
过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
A.10 B.8 C.6 D.4
将函数 的图象向_________单位可得到函数
的图象向_________单位可得到函数 的图象。
的图象。
A.向左平移 |
B.向右平移 |
C.向右平移 |
D.向左平移 |
已知 是非零向量且满足
是非零向量且满足 则
则 的形状是( )
的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等边三角形 |
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域 内植树,第一棵树在
内植树,第一棵树在 点,第二棵树在
点,第二棵树在 点,第三棵树在
点,第三棵树在 点,第四棵树在
点,第四棵树在 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
| A.(9,44) | B.(10,44) | C.(10.43) | D.(11,43) |
已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于 两点,
两点, 为坐标原点.若双曲线的离心率为2,
为坐标原点.若双曲线的离心率为2, 的面积为
的面积为 ,则
,则 _________.
_________.
对于三次函数 (
( ),给出定义:设
),给出定义:设 是函数
是函数 的导数,
的导数, 是函数
是函数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数
的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数 ,请你根据上面探究结果,计算
,请你根据上面探究结果,计算
 +
+ …+
…+ +
+ = .
= .
设三角形ABC的内角 所对的边长分别为
所对的边长分别为 ,
, ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若AC=BC,且 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的极值,并指出是极大值还是极小值;
的极值,并指出是极大值还是极小值;
(Ⅱ)若 ,求证:在区间
,求证:在区间 上,函数
上,函数 的图像在函数
的图像在函数 的图像的下方.
的图像的下方.
等差数列 中,
中, ,公差
,公差 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列 的第2项,第3项,第4项.
的第2项,第3项,第4项.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设数列 对任意自然数均有
对任意自然数均有 成立,求
成立,求 的值.
的值.
已知椭圆 的中心在原点
的中心在原点 ,离心率
,离心率 ,右焦点为
,右焦点为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆的上顶点为 ,在椭圆
,在椭圆 上是否存在点
上是否存在点 ,使得向量
,使得向量 与
与 共线?若存在,求直线
共线?若存在,求直线 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.
设数列 的前
的前 项和为
项和为 ,已知
,已知 (n∈N*).
(n∈N*).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证:当x>0时,
(Ⅲ)令 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
.
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量 并有特征值λ2=-1及属于特征值-1的一个特征向量
并有特征值λ2=-1及属于特征值-1的一个特征向量 (1)求矩阵M.(2)求M5α.
(1)求矩阵M.(2)求M5α.
已知直线l过点P(2,0),斜率为 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
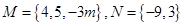 ,若
,若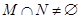 ,则实数
,则实数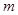 的值为( )
的值为( )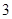 或
或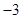
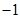
 中,
中, ,
, 则
则 =( )
=( )
 ,则
,则 ( )
( )


 的一个焦点在圆
的一个焦点在圆 上,则双曲线的渐近线方程为( )
上,则双曲线的渐近线方程为( )



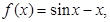
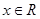 ,则
,则 、
、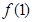 、
、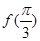 的大小关系( )
的大小关系( ) 的解集为{
的解集为{ ,则
,则 的解集为 .
的解集为 . ,则f
,则f 等于
等于  满足约束条件
满足约束条件 若目标函数
若目标函数 的最大值为1,则
的最大值为1,则 的最小值为_________.
的最小值为_________.
 对任意x∈R恒成立,求m的取值范围.
对任意x∈R恒成立,求m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号