[辽宁]2014届辽宁省抚顺市六校联合体高三上学期期中考试文科数学试卷
已知向量a=(1,1),b=(2,x).若a+b与4b-2a平行,则实数x的值是( )
| A.-2 | B.0 | C.1 | D.2 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h随时间t变化的可能图象是( )
设函数f(x)=Asin( )(A>0,
)(A>0, >0,-
>0,- <
< <
< )的图象关于直线x=
)的图象关于直线x= 对称,且周期为π,则f(x)( )
对称,且周期为π,则f(x)( )
A.图象过点(0, ) ) |
B.最大值为-A |
| C.图象关于(π,0)对称 | D.在[ , , ]上是减函数 ]上是减函数 |
已知R上可导函数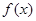 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集为( )
的解集为( )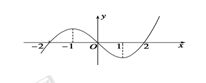
| A.(-∞,-2)∪(1,+∞) |
| B.(-∞,-2)∪(1,2) |
| C.(-∞,-1)∪(-1,0)∪(2,+∞) |
| D.(-∞,-1)∪(-1,1)∪(3,+∞) |
从抛物线 图像上一点
图像上一点 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为 ,且
,且 ,设抛物线焦点为
,设抛物线焦点为 ,则
,则 的面积为( )
的面积为( )
| A.10 | B.8 | C.6 | D.4 |
某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是__________.
已知正四棱锥O-ABCD的体积为 ,底面边长为
,底面边长为 ,则以O为球心,OA为半径的球的表面积_________.
,则以O为球心,OA为半径的球的表面积_________.
已知点 、
、 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、 两点,若
两点,若 为锐角三角形,则该双曲线的离心率
为锐角三角形,则该双曲线的离心率 的取值范围是____________.
的取值范围是____________.
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
(Ⅰ)求 ,
, ;
;
(Ⅱ)若从高二、高三年级抽取的人中选 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率.
已知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知动直线 与椭圆
与椭圆 相交于
相交于 、
、 两点. ①若线段
两点. ①若线段 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;②若点
的值;②若点 ,求证:
,求证: 为定值.
为定值.
已知函数 是R上的奇函数,当
是R上的奇函数,当 时
时 取得极值
取得极值 .
.
(I)求 的单调区间和极大值
的单调区间和极大值
(II)证明对任意
 不等式
不等式 恒成立.
恒成立.
如图, 是以
是以 为直径的半圆
为直径的半圆 上的一点,过
上的一点,过 的直线交直线
的直线交直线 于
于 ,交过A点的切线于
,交过A点的切线于 ,
, .
.
(Ⅰ)求证: 是圆
是圆 的切线;
的切线;
(Ⅱ)如果 ,求
,求 .
.
平面直角坐标系中,直线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线 与曲线
与曲线 相交于
相交于 两点,求
两点,求 .
.
 ,
, ,
, ,则
,则 =( )
=( )



 的值是( )
的值是( )

 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值等于( )
的值等于( ) 的值是( )
的值是( )




 是正数,且满足
是正数,且满足 .那么
.那么 的取值范围是( )
的取值范围是( )



 在
在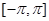 的图像大致为( )
的图像大致为( )
 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且 ,则方程
,则方程 在区间(0,6)内解的个数的最小值是 .
在区间(0,6)内解的个数的最小值是 .
 求
求 的值域;
的值域; 求
求 的值.
的值. 中,
中, ,
, ,且
,且 是
是 中点.
中点.
 平面
平面 ;
; 平面
平面 .
. .
. ;
; 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号