福建省四地六校联考高三上学期第二次月考文科数学卷
设条件
 条件
条件
 那么p是q的 ( )
那么p是q的 ( )
A.充分不必要条件 C.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
设向量 与
与 是两个不共线向量,且向量
是两个不共线向量,且向量 +
+
 与-(
与-( -2
-2 )共线,则
)共线,则 =( )
=( )
| A.0 | B.-1 | C.-2 | D.-0.5 |
已知正整数a、b满足 ( )
( )
| A.(5,10) | B.(6,6) | C.(10,5) | D.(7,2) |
将n2(n≥3)个正整数1,2,3,…,n2填入n×n方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,记f(n)为n阶幻方对角线上数的和。如下表所示
| 8 |
1 |
6 |
| 3 |
5 |
7 |
| 4 |
9 |
2 |
就是一个3阶幻方,可知f(3)=15,则f(n)= ( )
| A.n(n2+1) | B.n2(n+1)-3 | C.n2(n2+1) | D.n(n2+1) |
正整数 的三次幂可拆分成几个连续奇数的和,如右图所示,若
的三次幂可拆分成几个连续奇数的和,如右图所示,若 的“拆分数”中有一个数是2009,则
的“拆分数”中有一个数是2009,则 的值为 .
的值为 .
(本小题满分12分)设数列{an}的前n项和为Sn,
(I)求证数列{an}为等差数列;
(II)设数列 的前n项和为Tn,求
的前n项和为Tn,求 .
.
(本小题满分12分)
已知函数 .
.
(I)将函数f(x)写成f(x)= (
( )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c所对的角分别为A ,B ,C且满足 ,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.
,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.
(本小题满分12分)
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4 200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.
(1)设总造价为S元,AD长为 m,试建立S与x的函数关系;
m,试建立S与x的函数关系;
(2)当x为何值时,S最小?并求这个最小值.
(本小题满分12分)
设函数
 ,
,  图象的一条对称轴是直线
图象的一条对称轴是直线 .
.
(I)求 ;
;
(II)求函数 的单调增区间;
的单调增区间;
(Ⅲ)画出函数 在区间
在区间 上的图象.
上的图象.
(本小题满分12分)
已知命题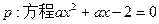 在[-1,1]上有解,
在[-1,1]上有解,
命题q:只有一个实数x满足:
(I)若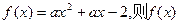 的图象必定过两定点,试写出这两定点的坐标.
的图象必定过两定点,试写出这两定点的坐标.
(只需写出两点坐标即可,不要过程);
(Ⅱ)若命题“p或q”为假命题,求实数a 的取值范围。
 的虚部为( )
的虚部为( ) 

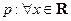 ,
,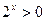 ,则( )
,则( )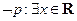 ,
,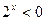
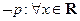 ,
,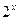 ≤
≤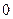
 中,已知
中,已知 ,那么
,那么 =" "
=" " ,则
,则 等于( )
等于( )



 ,若
,若 ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )


 与
与 的夹角为
的夹角为 ,
, ,则
,则 等于( )
等于( )


 是定义在R上的奇函数,它在
是定义在R上的奇函数,它在 上有
上有 ,那么下述式子中正确的是 ( )
,那么下述式子中正确的是 ( ) 



 ,
,
 ,
, 则
则 ( )
( )
 的公比
的公比 ,前n项和为
,前n项和为 ,则
,则 的值为 .
的值为 . 中,角A、B、C的对边边长分别是a、b、c,若
中,角A、B、C的对边边长分别是a、b、c,若 ,
, ,
, ,则c的值为 .
,则c的值为 . 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为 .
的最小值为 .  在
在 ,
, 处取得极值,且
处取得极值,且 .
. ,求
,求 的值,并求
的值,并求 的单调区间;
的单调区间; ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号