[江苏]2014届江苏省徐州市高三第一学期期中数学试卷
已知 ,函数
,函数 .
.
(1)当 时,写出函数
时,写出函数 的单调递增区间;
的单调递增区间;
(2)当 时,求函数
时,求函数 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;
(3)设 ,函数
,函数 在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
来源:2014届江苏省徐州市高三第一学期期中数学试卷
如图,某生态园欲把一块四边形地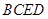 辟为水果园,其中
辟为水果园,其中 ,
, 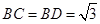 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 将四边形
将四边形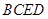 分成面积相等的两部分,设
分成面积相等的两部分,设 .
.
(1)求 的关系式;
的关系式;
(2)如果 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求 的长的最小值;
的长的最小值;
(3)如果 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么 的位置在哪里?
的位置在哪里?
来源:2014届江苏省徐州市高三第一学期期中数学试卷
已知等比数列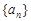 满足
满足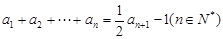 .
.
(1)求数列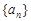 的通项公式;
的通项公式;
(2)在 与
与 之间插入
之间插入 个数连同
个数连同 与
与 按原顺序组成一个公差为
按原顺序组成一个公差为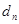 (
(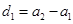 )的等差数列.
)的等差数列.
①设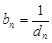 ,求数列
,求数列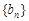 的前
的前 和
和 ;
;
②在数列 中是否存在三项
中是否存在三项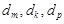 (其中
(其中 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
来源:2014届江苏省徐州市高三第一学期期中数学试卷
 ,则
,则 .
. 的虚部是 .
的虚部是 . ”是“
”是“ ”的 条件.(填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一)
”的 条件.(填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一) ,圆心角为120°,则扇形的面积为 .
,圆心角为120°,则扇形的面积为 . ,则
,则 的最小值是 .
的最小值是 . (其中
(其中 )在
)在 处的切线方程为 .
处的切线方程为 . 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知 ,
, ,则
,则 .
. 在
在 内有相异两解
内有相异两解 ,则
,则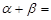 .
. 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,A = 45°,B = 60°,那么△ABC的面积
,A = 45°,B = 60°,那么△ABC的面积 .
. 对一切
对一切 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 . , 若函数
, 若函数 有3个零点,则实数
有3个零点,则实数 的取值范围是 .
的取值范围是 . 满足公比
满足公比 ,
, ,且{
,且{ }中的任意两项之积也是该数列中的一项,若
}中的任意两项之积也是该数列中的一项,若 ,则
,则 的所有可能取值的集合为 .
的所有可能取值的集合为 . ,且
,且 ,则
,则 .
. 满足
满足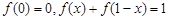 ,
, ,且当
,且当 时,
时, ,则
,则 .
. 满足:
满足: ,
, .
. 及
及 ,求数列
,求数列 的前n项和
的前n项和 .
. ,
, ,
, 为锐角.
为锐角. ,求
,求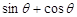 的值;
的值; ,求
,求 的值.
的值. .
. 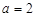 时,求函数
时,求函数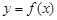 在
在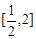 上的最大值;
上的最大值; ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;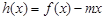 的图象与
的图象与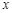 轴交于两点
轴交于两点 ,且
,且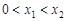 ,又
,又 是
是 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件 ,证明:
,证明: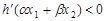 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号