[内蒙古]2013年初中毕业升学考试(内蒙古包头卷)数学
若|a|=﹣a,则实数a在数轴上的对应点一定在
| A.原点左侧 | B.原点或原点左侧 | C.原点右侧 | D.原点或原点右侧 |
已知方程x2﹣2x﹣1=0,则此方程
| A.无实数根 | B.两根之和为﹣2 |
| C.两根之积为﹣1 | D.有一根为 |
一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数据的众数为
| A.6 | B.8 | C.9 | D.10 |
下列事件中是必然事件的是
| A.在一个等式两边同时除以同一个数,结果仍为等式 |
| B.两个相似图形一定是位似图形 |
| C.平移后的图形与原来图形对应线段相等 |
| D.随机抛掷一枚质地均匀的硬币,落地后正面一定朝上 |
用一个圆心角为120°,半径为2的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为
A. |
B. |
C. |
D. |
如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是
| A.S1>S2 | B.S1=S2 | C.S1<S2 | D.3S1=2S2 |
已知下列命题:
①若a>b,则c﹣a<c﹣b;
②若a>0,则 ;
;
③对角线互相平行且相等的四边形是菱形;
④如果两条弧相等,那么它们所对的圆心角相等.
其中原命题与逆命题均为真命题的个数是
| A.4个 | B.3个 | C.2个 | D.1个 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2.其中正确的结论是
| A.①② | B.①③ | C.①③④ | D.①②③④ |
某次射击训练中,一小组的成绩如表所示:已知该小组的平均成绩为8环,那么成绩为9环的人数是 .
| 环数 |
7 |
8 |
9 |
| 人数 |
3 |
4 |
|
设有反比例函数 ,(x1,y1),(x2,y2)为其图象上两点,若x1<0<x2,y1>y2,则k的取值范围 .
,(x1,y1),(x2,y2)为其图象上两点,若x1<0<x2,y1>y2,则k的取值范围 .
如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为 .
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 .
如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.
甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜.如果指针落在分割线上,则需要重新转动转盘.
(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?试说明理由.
如图,一根长 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
(1)求OB的长;
(2)当AA′=1米时,求BB′的长.
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14400元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当 时,求
时,求 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF= OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG= BG.
BG.








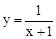 中,自变量x的取值范围是
中,自变量x的取值范围是 ,其结果是
,其结果是



 .
.
 (x﹣m)>3﹣m的解集为x>1,则m的值为 .
(x﹣m)>3﹣m的解集为x>1,则m的值为 . 的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
 ,0)和点F(0,
,0)和点F(0, ),直线l经过E、F两点,点G是线段BD的中点.
),直线l经过E、F两点,点G是线段BD的中点. 粤公网安备 44130202000953号
粤公网安备 44130202000953号