河南省郑州市智林学校高二下学期期末考试数学试卷(文科)
在航天员进行的一项太空实验中,要先后实施6个程序,其中程序 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A. 种 种 |
B. 种 种 |
C. 种 种 |
D. 种 种 |
已知函数 表示过原点的曲线,且在
表示过原点的曲线,且在 处的切线的倾斜角均为
处的切线的倾斜角均为 ,有以下命题:
,有以下命题:
① 的解析式为
的解析式为 ;
;
② 的极值点有且只有一个;
的极值点有且只有一个;
③ 的最大值与最小值之和等于零;
的最大值与最小值之和等于零;
其中正确命题的序号为_ .
(本小题满分10分)经过点 ,倾斜角为
,倾斜角为 的直线
的直线 ,与曲线
,与曲线 :
: (
( 为参数)相交于
为参数)相交于 两点.
两点.
(1)写出直线 的参数方程,并求当
的参数方程,并求当 时弦
时弦 的长;[
的长;[
(2)当 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;
(3)当 时,求直线
时,求直线 的方程;
的方程;
(4)当 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程.
(本小题满分9分)设在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片,标号分别记为 ,设随机变量
,设随机变量 .
.
(1)写出 的可能取值,并求随机变量
的可能取值,并求随机变量 的最大值;
的最大值;
(2)求事件“ 取得最大值”的概率;
取得最大值”的概率;
(3)求 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(本小题满分9分)如图,已知⊙ 与⊙
与⊙ 外
外
切于点 ,
, 是两圆的外公切线,
是两圆的外公切线, ,
, 为切
为切
点, 与
与 的延长线相交于点
的延长线相交于点 ,延长
,延长
交⊙ 于 点
于 点 ,点
,点 在
在 延长线上.
延长线上.
(1)求证: 是直角三角形;
是直角三角形;
(2)若 ,试判断
,试判断 与
与 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.
(3)在(2)的条件下,若 ,
, ,求
,求 的值.
的值.
 等于 ( )
等于 ( )



 是纯虚数,则
是纯虚数,则 的值为 ( )
的值为 ( )



 ,则它的导函数是 ( )
,则它的导函数是 ( )



 ( )
( )




 经过伸缩变换T得到曲线
经过伸缩变换T得到曲线 ,那么直线
,那么直线 经过伸缩变换T得到的直线方程为 ( )
经过伸缩变换T得到的直线方程为 ( )



 的圆心坐标是 ( )
的圆心坐标是 ( ) B
B  C
C  D
D 
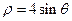 相切的一条直线的方程为 ( )
相切的一条直线的方程为 ( )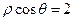 B
B 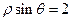
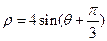 D
D 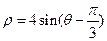
 服从正态分布
服从正态分布 ,
, ,则
,则 等于 ( )
等于 ( )



 则在这段时间内吊灯能照明的概率是 ( )
则在这段时间内吊灯能照明的概率是 ( )



 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有 ( )
,则必有 ( ) B
B 
 D
D 
 的最大值是 .
的最大值是 . ,
, ,
, 所围成的图形面积为 .
所围成的图形面积为 . 的展开式中含
的展开式中含 的项的系数是 .
的项的系数是 .

 .
. 时,解关于
时,解关于 的不等式
的不等式 ;
; ,
, 的取值范围.
的取值范围. ,其中
,其中 为正整数.
为正整数. ,
, ,
, 的值;
的值; 的正整数
的正整数
 在
在 处取得极值
处取得极值 ,其中
,其中 为常数.
为常数. 的值;
的值;  的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号