[山东]2013届山东临沂高三5月高考模拟文科数学试卷
某班共有52人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号同学在样本中,那么样本中还有一个同学的学号是( )
| A.10 | B.11 | C.12 | D.16 |
将函数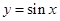 的图象向右平移
的图象向右平移 个单位长度,再向上平移1个单位长度,则所得的图象对应的解析式为( )
个单位长度,再向上平移1个单位长度,则所得的图象对应的解析式为( )
A.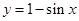 |
B.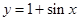 |
C.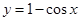 |
D.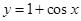 |
阅读如图所示的程序框图,若输入变量n为100,则输出变量S为( )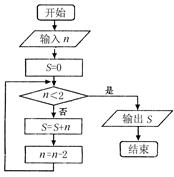
| A.2500 | B.2550 | C.2600 | D.2650 |
给出如下四个命题:
①若“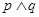 ”为假命题,则
”为假命题,则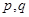 均为假命题;
均为假命题;
②命题“若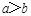 ,则
,则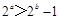 ”的否命题为“若
”的否命题为“若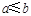 ,则
,则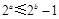 ”;
”;
③命题“任意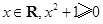 ”的否定是“存在
”的否定是“存在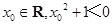 ”;
”;
④在 中,“
中,“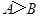 ”是“
”是“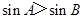 ”的充要条件.
”的充要条件.
其中不正确命题的个数是 ( )
| A.4 | B.3 | C.2 | D.1 |
多面体MN-ABCD的底面ABCD为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则AM的长( )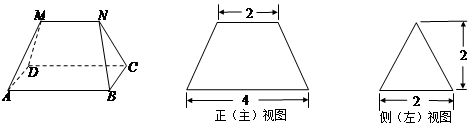
A.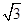 |
B.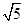 |
C.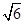 |
D.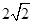 |
已知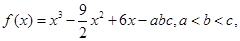 且
且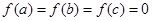 ,现给出如下结论:
,现给出如下结论:
①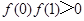 ;②
;②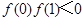 ;③
;③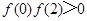 ;④
;④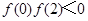 .其中正确结论的序号为:( )
.其中正确结论的序号为:( )
| A.①③ | B.①④ | C.②④ | D.②③ |
假设关于某设备的使用年限 和所支出的维修费
和所支出的维修费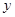 (万元)有如下的统计资料:
(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
由资料可知y和x呈线性相关关系,由表中数据算出线性回归方程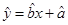 中的
中的 据此估计,使用年限为10年时的维修费用是 万元.
据此估计,使用年限为10年时的维修费用是 万元.
已知双曲线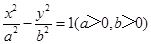 的左顶点与抛物线
的左顶点与抛物线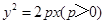 的焦点的距离为
的焦点的距离为
4,且双曲线的一条渐近线与抛物线准线的交点坐标为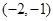 ,则双曲线的焦距为 .
,则双曲线的焦距为 .
已知点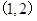 是函数
是函数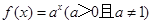 的图象上一点,数列
的图象上一点,数列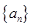 的前n项和
的前n项和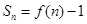 .
.
(Ⅰ)求数列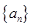 的通项公式;
的通项公式;
(Ⅱ)将数列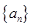 前2013项中的第3项,第6项, ,第3k项删去,求数列
前2013项中的第3项,第6项, ,第3k项删去,求数列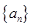 前2013项中剩余项的和.
前2013项中剩余项的和.
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
 (i是虚数单位),则
(i是虚数单位),则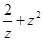 等于( )
等于( )


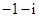
 则集合B可能是( )
则集合B可能是( )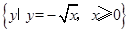
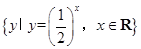
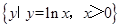
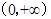 上单调递增的函数是( )
上单调递增的函数是( )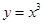
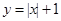
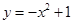
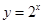
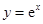 在点
在点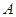 处的切线与直线
处的切线与直线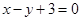 平行,则点
平行,则点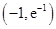
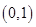
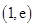
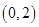
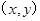 满足
满足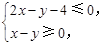 若目标函数
若目标函数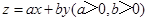 的最大值是4,则
的最大值是4,则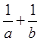 的最小值为( )
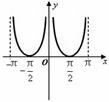
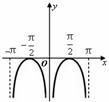
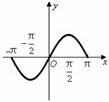
的最小值为( )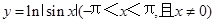 的图象大致是( )
的图象大致是( )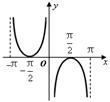
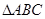 的边
的边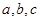 满足
满足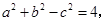 且C=60°,则
且C=60°,则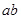 的值为 .
的值为 .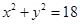 ,直线l:
,直线l: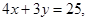 则圆
则圆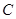 上任一点到直线
上任一点到直线 的距离小于2的概率为 .
的距离小于2的概率为 .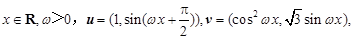 函数
函数 的最小正周期为
的最小正周期为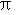 .
.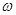 的值;
的值;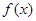 在区间
在区间 上的值域.
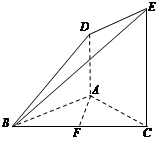
上的值域.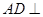 平面
平面 凸多面体
凸多面体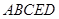 的体积为
的体积为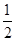 ,
,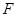 为
为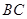 的中点.
的中点. 平面
平面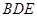 ;
;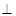 平面
平面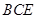 .
. 
 .
. 的单调区间;
的单调区间; ,且
,且 在区间
在区间 内存在极值,求整数
内存在极值,求整数 的值.
的值. 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号