[北京]2013年北京市顺义区中考二模数学试卷
正方形 ,
, 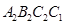 ,,
,,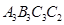 , …按如图所示的方式放置.点
, …按如图所示的方式放置.点 ,
,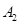 ,
,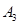 ,…和点
,…和点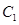 ,
,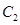 ,
,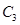 …分别在直线
…分别在直线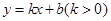 和
和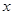 轴上,已知点
轴上,已知点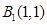 ,
, ,则点
,则点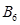 的坐标是 ,点
的坐标是 ,点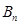 的坐标是 .
的坐标是 .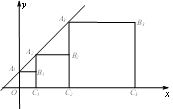
列方程或方程组解应用题:
某企业向四川雅安地震灾区捐助价值17.6万元的甲、乙两种帐篷共200顶,已知甲种帐篷每顶800元,乙种帐篷每顶1000元,问甲、乙两种帐篷各多少顶?
如图,在平面直角坐标系 中,一次函数
中,一次函数 的图象与
的图象与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,与反比例函数图象相交于点
,与反比例函数图象相交于点 ,且
,且 .
.
(1)求反比例函数的解析式;
(2)若点 在
在 轴上,且
轴上,且 的面积等于12,直接写出点
的面积等于12,直接写出点 的坐标.
的坐标.
已知:如图, 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是 外一点,PA切
外一点,PA切 于点A,且PA=PB.
于点A,且PA=PB.
(1)求证:PB是 的切线;
的切线;
(2)已知PA= ,BC=2,求
,BC=2,求 的半径.
的半径.
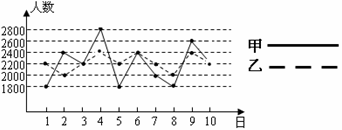
甲、乙两学校都选派相同人数的学生参加综合素质测试,测试结束后,发现每名参赛学生的成绩都是70分、80分、90分、100分这四种成绩中的一种,并且甲、乙两学校的学生获得100分的人数也相等.根据甲学校学生成绩的条形统计图和乙学校学生成绩的扇形统计图,解答下列问题:

(1)求甲学校学生获得100分的人数,并补全统计图;
(2)分别求出甲、乙两学校学生这次综合素质测试所得分数的中位数和平均数,以此比较哪个学校的学生这次测试的成绩更好些.
问题:如果存在一组平行线 ,请你猜想是否可以作等边三角形
,请你猜想是否可以作等边三角形 使其三个顶点分别在
使其三个顶点分别在 上.
上.
小明同学的解答如下:如图1所示,过点 作
作 于
于 ,作
,作 ,且
,且 ,过点
,过点 作
作 交直线
交直线 于点
于点 ,在直线
,在直线 上取点
上取点 使
使 ,则
,则 为所求.
为所求.

(1)请你参考小明的作法,在图2中作一个等腰直角三角形 使其三个顶点分别在
使其三个顶点分别在 上,点
上,点 为直角顶点;
为直角顶点;
(2)若直线 之间的距离为1,
之间的距离为1, 之间的距离为2,则在图2中,
之间的距离为2,则在图2中, ,在图1中,
,在图1中, .
.
已知抛物线 .
. 
(1)求证:无论 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点;
(2)若 为整数,当关于x的方程
为整数,当关于x的方程 的两个有理数根都在
的两个有理数根都在 与
与 之间(不包括-1、
之间(不包括-1、 )时,求
)时,求 的值.
的值.
(3)在(2)的条件下,将抛物线 在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象
在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象 ,再将图象
,再将图象 向上平移
向上平移 个单位,若图象
个单位,若图象 与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是 .
与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是 .
如图,直线 与线段
与线段 相交于点
相交于点 ,点
,点 和点
和点 在直线
在直线 上,且
上,且 .
.
(1)如图1所示,当点 与点
与点 重合时 ,且
重合时 ,且 ,请写出
,请写出 与
与 的数量关系和位置关系;
的数量关系和位置关系;
(2)将图1中的 绕点
绕点 顺时针旋转到如图2所示的位置,
顺时针旋转到如图2所示的位置, ,(1)中的
,(1)中的 与
与 的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)将图2中的 拉长为
拉长为 的
的 倍得到如图3,求
倍得到如图3,求 的值.
的值.

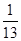
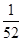
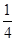
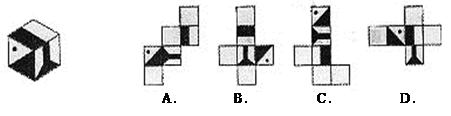
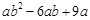 分解因式,下列结果中正确的是
分解因式,下列结果中正确的是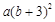
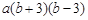
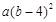
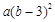
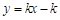 与
与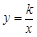 (
(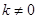 )在同一直角坐标系中的图象可能是
)在同一直角坐标系中的图象可能是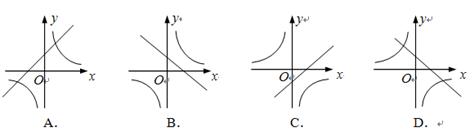
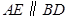 ,
,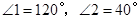 ,则
,则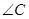 的度数是
的度数是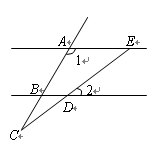
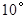

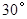
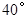
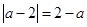 ,则
,则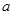 的取值范围是
的取值范围是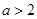
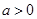
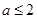
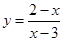 中,自变量
中,自变量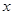 的取值范围是 .
的取值范围是 .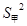
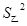 .
.
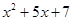 化为
化为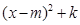 的形式,其中
的形式,其中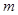 、
、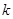 为常数,则
为常数,则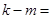 .
.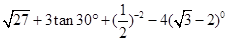 .
. .
. ,求代数式
,求代数式 的值.
的值. 中,
中, ,
, ,
, 是过点
是过点 的一条直线,
的一条直线, 于
于 ,
, 于
于 ,求证:
,求证:  .
.
 中,对角线AC、BD相交于点E,
中,对角线AC、BD相交于点E, ,
, ,
, . 求对角线
. 求对角线 的长和
的长和 的面积.
的面积.
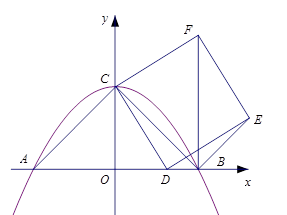
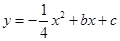 与
与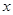 轴交于
轴交于 两点,与
两点,与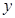 轴交于点
轴交于点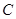 ,连结
,连结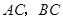 ,
,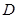 是线段
是线段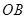 上一动点,以
上一动点,以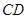 为一边向右侧作正方形
为一边向右侧作正方形 ,连结
,连结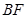 .若
.若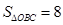 ,
,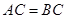 .
.
 ;
;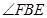 的度数;
的度数;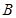 时,点
时,点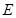 也随着运动,则点
也随着运动,则点 粤公网安备 44130202000953号
粤公网安备 44130202000953号