2010年全国统一高考理科数学试卷(重庆卷)
某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为
,则该队员每次罚球的命中率为 .
在甲、乙等6个单位参加的一次"唱读讲传"演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……6),求:
(I)甲、乙两单位的演出序号至少有一个为奇数的概率;
(II)甲、乙两单位之间的演出单位个数
的分布列与期望。
已知函数
其中实数
.
(I)若
,求曲线
在点
处的切线方程;
(II)若
在
处取得极值,试讨论
的单调性.
如图,四棱锥 中,底面 为矩形, 底面 , ,点 是棱 的中点。
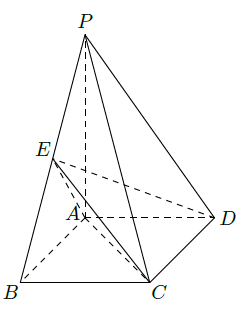
(
)求直线
与平面
的距离;
(
)若
,求二面角
的平面角的余弦值。
已知以原点
为中心,
为右焦点的双曲线
的离心率
.
(I)求双曲线
的标准方程及其渐近线方程;
(II)如题图,已知过点
的直线
与过点
(其中
)的直线
的交点
在双曲线
上,直线
与两条渐近线分别交与
两点,求
的面积.

在数列
中,
,
,其中实数
.
(1)求 的通项公式;
(2)若对一切 有 ,求 的取值范围。
某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有( )
| A. | 504种 |
| B. | 960种 |
| C. | 1008种 |
| D. | 1108种 |
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )
| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
函数的图象()
| A. |
关于原点对称 |
B. |
关于直线对称 |
| C. |
关于轴对称 |
D. |
关于轴对称 |
直线
与圆心为D的圆
交与
两点,则直线
与
的倾斜角之和为( ).

| A. |
|
B. |
|
C. |
|
D. |
|

 粤公网安备 44130202000953号
粤公网安备 44130202000953号